유전 알고리즘의 연산자를 다시 살펴보고, 파이썬으로 타겟 문장을 찾는 간단한 유전 알고리즘을 구현해봅니다.
Introduction
유전 알고리즘 은 생물들의 진화 현상을 모방하여 최적화 문제 를 풀기 위한 알고리즘이다.
다윈의 진화론 은 생물의 진화를 설명하는 가장 유명한 이론이다. 다윈은 진화론의 핵심이 되는 개념으로 적자생존의 법칙(Survival of the fittest) 을 제시했다. 이 법칙에 따르면, 시간이 지남에 따라 변화하는 자연 환경에 더욱 잘 적응하는 생물만이 살아남는다. 자연계의 생물들은 변화하는 환경에 적응하기 위해 다양한 방법으로 진화한다. 같은 종끼리의 교배로 부모 세대보다 진화된 자손을 남기기도 하고, 환경에 강인한 돌연변이의 출현으로 기존에 서식하던 종의 자리를 대체하기도 한다. 생물들은 이러한 진화의 과정을 수없이 많은 시간동안 반복해오면서 변화하는 지구 환경에 적응해왔다.
유전 알고리즘은 자연에서 일어나는 유전과 진화 과정을 모방하여 최적화 문제 해결에 사용한다. 최적해의 후보가 될 수 있는 수많은 해들의 집단을 운용하면서 진화의 과정을 시뮬레이션한다. 해의 진화를 계속 일으키다보면, 결과적으로 주어진 문제의 최적해를 구해낼 수 있을 것이다.
유전 알고리즘의 용어들
생물의 진화를 모방한 알고리즘인 만큼, 유전 알고리즘에는 진화론과 유전학의 용어를 차용해 온 부분이 많다.
생물의 유전에 관여하는 물질을 염색체(Chronosome) 라고 한다. 생물 개체의 유전은 염색체들끼리의 재조합과 일정한 확률의 돌연변이를 거쳐, 새로운 염색체를 만듬으로써 이루어진다. 이와 비슷하게, 유전 알고리즘에서는 문제 해결 중에 생기는 임의의 해를 염색체 또는 해 라고 한다. 생물의 염색체가 진화하는 것처럼, 유전 알고리즘의 염색체 또한 알고리즘이 진행됨에 따라 점점 진화할 것이다. 또한 자연에서는 생물 개체 집단 안의 개체의 수가 가변적이고 제한이 없다. 그러나 유전 알고리즘에서는 대부분의 경우 정해진 수의 염색체를 가진 집단을 운영한다. 이 염색체의 집단을 해집단(Population) 이라고 한다.
유전 알고리즘에서의 염색체는 보통 숫자의 배열이나 문자열의 형태이다. 해집단은 그것들을 모아놓은 집합일 것이다.

염색체 상에서 각각의 인자를 유전자(Gene) 이라고 한다. 유전자는 유전 알고리즘의 최소 단위로써, 하나의 해를 이루는 각 부분이 될 것이다. 유전 알고리즘에서 일어나는 대부분의 연산은 염색체 내의 유전자를 교체하는 단위에서 이루어진다. 염기와 같은 유전자의 하위 개념은 사용되지 않는다.

자연에서는 어떤 생물 개체군이 자식을 낳고 번성하며 시간이 흐르면, 부모 개체들이 늙거나 죽고 자식 개체들이 개체군의 운명을 이어가게 된다. 이러한 과정을 세대(Generation) 의 교체라고 부른다. 이와 비슷하게 유전 알고리즘에서도, 현재 운용중인 해집단을 현재 세대 라 하고, 유전 연산을 통하여 이전 세대로부터 만들어낸 새로운 해집단을 자식 세대 또는 다음 세대 라고 한다.
해의 적합도(fitness) 는 어떤 해가 얼마나 최적해에 가까운지를 보여준다. 또한 적합도가 높은 해를 보통 품질 이 좋은 해라고 한다. 적합도가 높을수록 최적해에 가까운 우수한 해라고 볼 수 있다. 대부분의 유전 알고리즘은 적합도가 높은 해가 더 많이 살아남아 자식 세대를 만들어내는 구조를 취하고 있다. 이는 자연에서 보이는 적자생존의 원칙과 비슷한 원리로, 세대를 거듭할 수록 우수한 해들만 해집단에 남을 수 있도록 한다.
적합도는 어떻게 정의하냐에 따라 달라질 수 있다. 문제에 따라 값이 높을수록 우수한 해일 수도 있고, 낮을수록 우수한 해일 수도 있다.

유전 연산
유전 알고리즘은 해집단의 해들에 대한 유전 연산들의 반복으로 이루어진다. 보통의 경우 아래의 네 가지 연산을 순서대로 반복한다.
선택 -> 교차 -> 변이 -> 대치
선택 연산자
선택 연산자는 자식 해를 만들기 위해서 부모 해를 선택하는 과정이다. 자연에서와 같이, 유전 알고리즘에서도 어떤 해가 문제의 최적해에 더욱 가까울수록 자손을 퍼트릴 확률이 높아진다. 다시 말해서, 선택(Selection) 될 확률이 높아진다는 것이다. 그래서 많은 경우, 선택 연산은 모든 해들의 적합도를 기반으로 이루어진다. 적합도가 높은 해가 선택될 확률을 더 높게 설정하는 것이다.
아래의 그림은, 대표적인 선택 방법인 룰렛 휠(Roulette Wheel) 선택을 보여준다. 선택의 과정이 마치 돌림판을 돌려 멈춘 곳의 해를 선택하는 것 같아 이러한 이름이 붙여졌다.
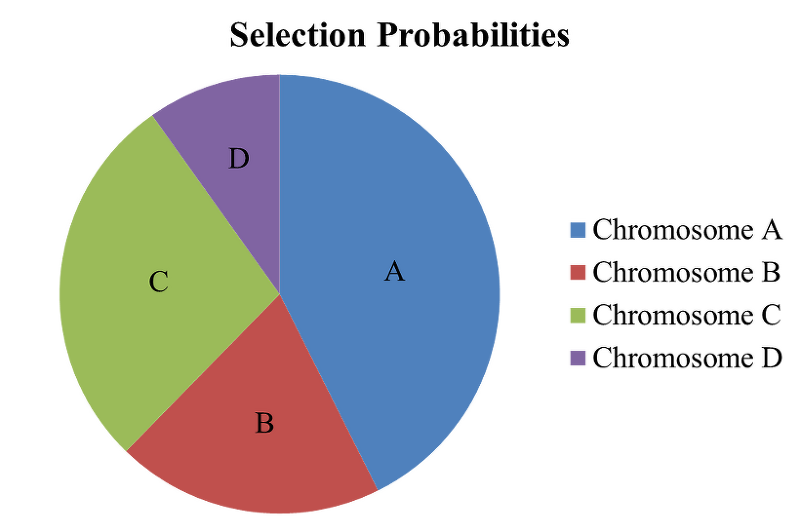
먼저 선택 후보 해들의 적합도를 계산하고, 적합도가 높을수록 많은 확률을 부여해 선택되도록 한다. 좋은 품질의 해가 가진 유전적 형질을 자손들에게 더 많이 남기도록 하는 것이다. 따라서 반복이 진행될수록 자연스럽게 우수한 해들만 남게 된다. 또한 계산된 적합도 수치가 동일해도, 룰렛 상에서의 크기 차이가 더 크게 나도록 선택 확률을 조정할 수도 있다. 가장 나쁜 해의 선택 확률과 가장 좋은 해의 선택 확률 사이의 차이가 커질수록, 좋은 품질의 해가 선택될 확률이 높아진다. 이러한 모양을 선택압 이 높다고 한다.
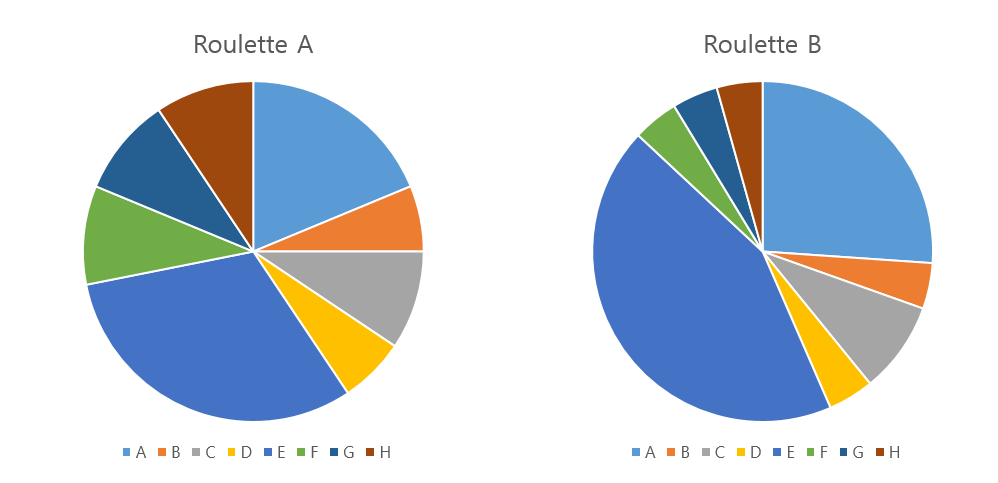
룰렛 휠 말고도 순위 기반 선택, 토너먼트 선택 등 다양한 선택 연산이 존재한다.
교차 연산자
교차(Crossover) 연산은 두 개 이상의 부모 염색체의 특징을 부분적으로 결합하여 새로운 자식 염색체를 만들어내는 연산이다. 자식 세대를 실제로 만들어내는 핵심적인 유전 연산이므로, 유전 알고리즘의 성능을 크게 좌우하는 연산이기도 하다. 그런 만큼 정말 많은 방법들이 존재한다.
가장 단순하면서도 널리 쓰이는 교차 연산이 바로 n점 교차 이다. 두 개의 부모 해를 선택한 후, n개의 자름선 위치를 설정한다. 그리고 자름선을 기준으로 하여, 두 부모 해에서 유전자들을 번갈아 가져온다. 직관적으로 두 부모 해의 특징을 합치는 방법이다. 아래의 그림은 1점 교차와 2점 교차의 예시를 보여 준다.
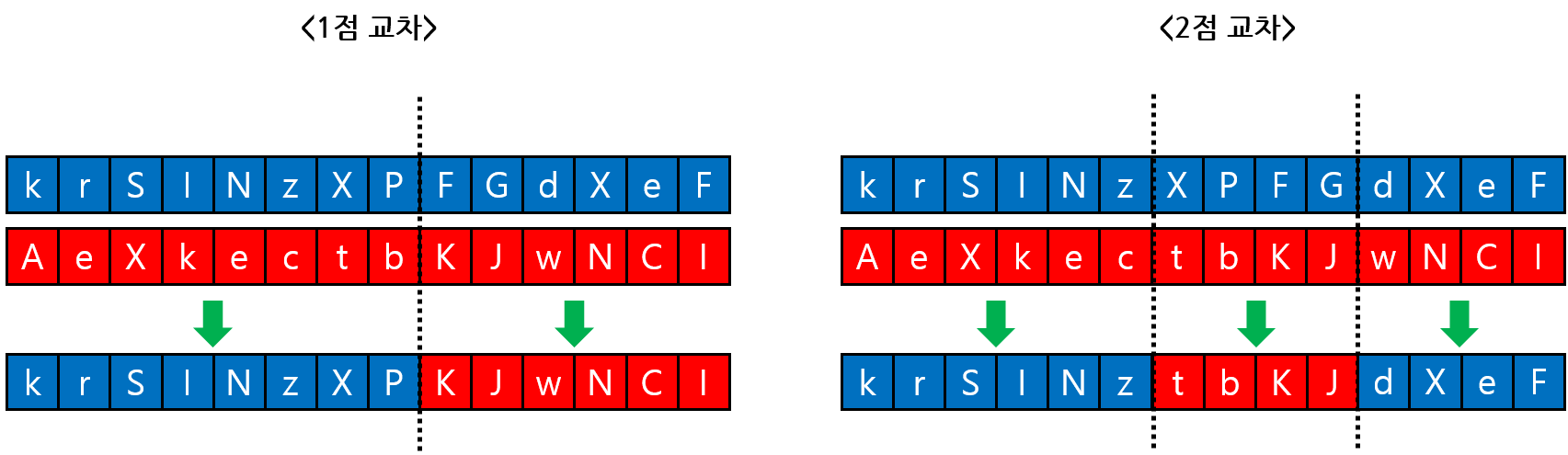
1점 교차는 하나의 자름선을 기준으로 부모 해를 나누어 가져오고, 2점 교차는 두 개의 자름선을 기준으로 나누어 가져온다. 자름선의 개수는 매우 민감한 파라미터이다. 자름선이 하나만 늘어나도 잘 수렴하던 알고리즘이 전혀 동작하지 않을 수 있다. 부모 해의 특징을 얼마나 많이 섞냐에 따라 해의 다양성 차이가 매우 커지기 때문이다.
위에서 소개한 n점 교차 말고도 균등 교차, 싸이클 교차, PMX 교차 등의 다양한 교차 연산들이 존재한다.
변이 연산자
변이(Mutation) 연산은, 자연에서 생물에게 일어나는 돌연변이와 같이 교차를 통해 만들어진 새로운 자식 해에게 일정 확률로 돌연변이를 일으켜주는 과정이다. 부모해에 없던 새로운 유전적 형질을 자식 해에게 심어주기 위해 변이를 일으킨다. 부모 해가 옳지 못한 방향으로 수렴하고 있을 때 적당히 일어나는 변이는, 알고리즘의 수렴이 새로운 방향으로 전환될 수 있게 해 준다. 아래의 그림은 가장 단순한 변이 연산의 예를 보여 준다.
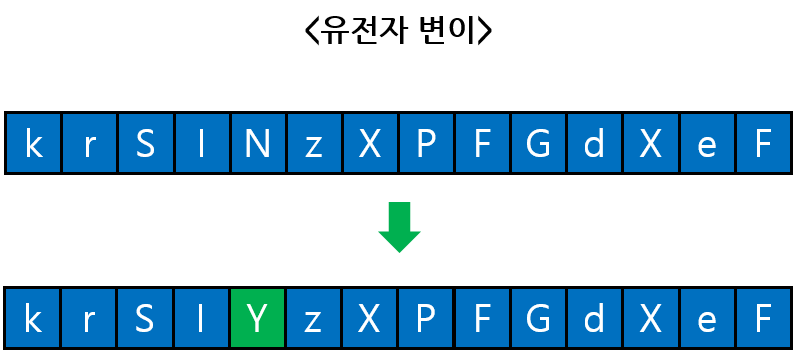
위의 그림에서는 문자열 형태 해의 일부를 무작위한 새로운 문자열로 변이시키는 모습을 보여준다. 두 부모 해에는 없던 새로운 알파벳들이 자식 해에 등장함으로써, 새로운 유전적 형질을 획득했다. 이 과정에서 훨씬 우수한 품질의 해를 얻을 확률도 있으므로, 적당한 변이는 알고리즘의 수렴을 돕는 역할을 한다. 보통의 경우 변이 연산은 확률적으로 일으킨다. 0과 1 사이 임의의 실수 난수를 생성하여, 미리 정한 임계값 미만의 수가 나오면 변이를 일으키는 방법이 흔하게 사용된다.
유전 알고리즘의 변이는 자연에서의 그것과 다르게, 대부분의 경우 해의 품질에 큰 영향을 미친다. 따라서 적당한 확률의 변이 연산 구현이 매우 중요하다.
대치 연산
대치(Replace) 연산은, 현재 세대의 해들을 새로이 만들어진 자식 세대의 해들로 교체하는 과정이다. 이 때, 자식 세대의 해가 부모 세대를 대체하는 비율을 세대 차(Generation Gap) 이라고 한다. 세대 차가 1에 가까울수록 부모 세대와 자식 세대간의 차이가 커져, 해집단의 특성이 빠르게 바뀔 것이다. 반대로 세대 차가 작아지면 해집단의 변화가 비교적 느릴 것이다. 세대 차의 설정에 따른 장단점이 존재하므로, 문제 상황에 맞게 잘 선택해야 한다.
아래 그림은 한 번의 세대 교체를 보여준다. 한 세대의 염색체 5개 중 4개가 새로운 자식해로 교체되므로, 세대차는 0.8일 것이다.

유전 알고리즘의 진행
유전 알고리즘의 진행을 간단하게 의사코드로 표현하면 아래와 같다.
초기 해집단 생성
종료 조건 만족시까지 반복 {
모든 해의 적합도 계산;
해집단에서 적절한 해를 선택;
해끼리의 교차를 통해 자식해 생성;
일정 확률로 해 변이;
새로 생성된 자식해들로 대치;
}
최적해 반환;
알고리즘을 설계하면서 먼저 해의 모습을 디자인하고, 해집단에서 운용할 해의 개수를 결정한다. 또한 종료 조건도 설정한다. 알고리즘의 시작 시에 초기 해집단을 생성하여 반복을 시작한다. 각 반복에서는 해들의 적합도를 계산하여 부모해를 선택하고, 교차와 변이를 거쳐 일정 개수의 자식해를 생성한다. 만들어진 자식해를 부모 해와 대치하여 다음 세대의 해집단을 만들어낸다. 이 과정을 반복하다 보면, 적합도가 종료 조건을 만족하는 특정한 해를 얻어낼 수 있을 것이다.
유전 알고리즘의 구현
이제 유전 알고리즘을 파이썬으로 직접 구현해보자. 유전 알고리즘은 보통 훨씬 복잡한 문제의 해를 실험적으로 구하기 위해 사용되지만, 실습을 위해 최대한 간단히 문제 상황을 정의하겠다.
우리는 랜덤한 문자열 해집단을 운용하는 유전 알고리즘을 구성하여, 최적해가 타겟 문자열과 같아지도록 해집단을 발전시킬 것이다. 문자열 해들을 목표 문자열과 최대한 비슷하게 진화시키는 것이 목표다. 목표 문자열은 Genetic Algorithm is cool 이다. 직접 유전 알고리즘을 디자인해서 목표 문자열을 찾아가 보자.
해와 적합도 디자인
목표 문자열 Genetic Algorithm is cool은 길이가 25인 문자열이다. 따라서 각각의 해 또한 25 길이의 문자열로 설정하겠다. 자연스럽게 적합도 계산 또한 각 문자 위치에서의 차이를 계산하는 문제로 바라볼 수 있게 된다. 알다시피 컴퓨터에서 하나의 문자는 결국 숫자로 표현되므로, 문자 사이의 수치적 차이를 계산할 수 있다.
초기 해집단 생성
알고리즘의 진행에 앞서, 초기 해집단을 생성한다. 해집단의 크기는 32개로 하자.
import random
target = 'Genetic Algorithm is cool'
len_chrono = len(target)
gen_size = 128
# randch: 무작위 문자 하나 생성 #
def randch():
return chr(random.randint(0, 255))
# make_random_chrono: 무작위 해 하나 생성 #
def make_random_chrono():
chrono = [randch() for _ in range(len_chrono)]
return ''.join(chrono)
# make_random_generation: 초기 해집단 생성 #
def make_random_generation():
return [make_random_chrono() for _ in range(gen_size)]
make_random_chronosome 함수가 랜덤한 문자열 해를 하나 생성하며, make_random_generation 함수로 초기 해집단을 생성한다.
적합도 함수 구현
본격적으로 알고리즘을 구성하기 전, 각 해의 적합도를 구하는 함수를 먼저 작성하자. 적합도 함수는 선택 알고리즘 및 해의 평가에서 사용된다. 목표 문자열과 해 문자열의 길이가 같으므로, 각각 같은 위치의 문자끼리의 아스키 값 차이 총합으로 적합도를 디자인하자. 아래와 같이 구현할 수 있다.
# get_fitness: 적합도 계산 #
def get_fitness(chrono):
fitness = 0
for i in range(len_chrono):
diff = abs(ord(target[i]) - ord(chrono[i]))
fitness += diff
return fitness
선택 알고리즘 구현
자식 해를 만들기 위해 부모 해집단에서 두 개의 해를 선택하는 알고리줌을 구현하자. Roulette Wheel 선택 알고리즘을 사용할 것이며, 선택압은 따로 고려하지 않는다. 해집단의 적합도를 모두 계산해 룰렛을 생성하고, 0에서 1 사이 실수 난수를 생성하여 선택을 위한 다트로 삼는다.
먼저 적합도를 기반으로 룰렛을 만드는 함수를 작성한다. 적합도가 낮을수록 우수한 해이기 때문에, 낮은 적합도를 가지는 해가 룰렛에서 더 넓은 면적을 차지하고 있어야 한다. 이를 코드로 아래와 같이 구현할 수 있다.
# make_roulette: 룰렛 휠 선택을 위한 룰렛 생성 #
# 적합도가 낮을수록 룰렛에서의 면적이 커짐 #
def make_roulette(generation):
fitnesses = [get_fitness(c) for c in generation]
max_fit, min_fit = max(fitnesses), min(fitnesses)
# 적합도를 뒤집어서 계산
sum_fitnesses_inverted = 0
for f in fitnesses:
sum_fitnesses_inverted += (max_fit + min_fit) - f
# 적합도를 뒤집어 룰렛 만들기
# 뒤집은 적합도 = (적합도 최대값 + 적합도 최소값) - 현재 적합도
prev_value = 0.0
roulette = [0.0]
for f in fitnesses:
fitness_inverted = (max_fit + min_fit) - f
value = float(fitness_inverted / sum_fitnesses_inverted)
roulette.append(prev_value + value)
prev_value += value
return roulette
이제 룰렛을 던져 해집단에서 해를 선택하는 함수를 구현하자.
# selection: 룰렛 휠 선택 연산 #
def selection(chronos, roulette):
selected_chrono = None
dart = random.random() # 다트 던지기
# 룰렛에서 해 선택
for idx in range(1, len(roulette)):
if dart < roulette[idx]:
selected_chrono = chronos[idx-1]
break
return selected_chrono
교차 알고리즘 구현
선택된 두 개의 부모 해를 교차하여 새로운 자식해를 생성한다. 문자열의 부분적인 특징을 적절히 섞어주기 위해서 1점 교차 연산을 사용하자. 임의의 정수 난수를 생성하여 자름선을 만들고, 자름선을 기준으로 두 부모 해를 교차해 가져오는 함수를 구현한다.
# crossover: 1점 교차 연산 #
def crossover(ca, cb):
cross_point = random.randint(0, len_chrono) # 무작위 자름선 생성
offspring = ca[:cross_point] + cb[cross_point:] # 양쪽 해에서 자름선 기준으로 가져옴
return offspring
변이 알고리즘 구현
해집단이 잘못된 방향으로만 수렴하는 것을 막기 위해서, 적절한 확률로 해에 변이를 일으켜준다. 문자열 안에서 하나의 문자를 골라 새로운 임의의 문자로 치환하는 방법을 사용할 것이다. 부모 해집단에서 나타나지 않았던 새로운 문자가 나타나면서, 해의 특성을 크게 바꿀 수 있는 기회가 될 것이다.
단순하게 무작위 위치의 문자를 선택하는 것보다, 문자의 값 차이가 가장 큰 위치의 문자를 변이시키는 것이 빠른 수렴에 더욱 도움을 줄 것이다. 이처럼 문제 상황과 해의 디자인에 따라 더 효율적인 유전 연산을 구현할 수 있다.
파이썬 코드로 아래와 같이 변이 연산을 구현할 수 있다.
# mutation: 변이 연산 #
def mutation(chrono):
mutated_chrono = chrono
propability = 0.03 # 변이 확률 0.03
if random.random() < propability:
# 문자 위치별 값 차이 리스트 생성
gene_diffs = []
for i in range(len_chrono):
diff = abs(ord(target[i]) - ord(chrono[i])) # 각 문자의 값 차이
gene_diffs.append(diff)
# 가장 크게 값이 차이나는 위치의 문자 변이
mutate_pos = gene_diffs.index(max(gene_diffs))
l_chrono = list(chrono)
l_chrono[mutate_pos] = randch()
mutated_chrono = ''.join(l_chrono)
# 변이된 문자열 반환
return mutated_chrono
세대 교체 과정 완성하기
위에서 구현한 유전 연산들로 부모 세대로부터 자식 세대 해집단을 생성하고, 대치 연산을 구현해 세대교체를 하는 과정을 완성해야 한다. 해집단의 변화 폭을 크게 가져가기 위해 세대차를 0.8로 크게 가져간다. 한 번의 세대 교체에 80%의 해가 교체된다는 것이다. 남은 20%는 부모 세대에서 가장 우수한 20%의 해를 그대로 물려받게 된다. 세대를 거듭할수록 우수한 품질의 해집단만 남을 것이다.
아래와 같이 한 번의 세대 교체를 구현할 수 있다.
# sort_generation: 적합도를 기반으로 해집단 정렬 #
def sort_generation(generation):
fitnesses = [get_fitness(c) for c in generation]
sorted_gen = [c for _, c in sorted(zip(fitnesses, generation))]
return sorted_gen
# make_offsprings: 부모 세대로부터 자식 세대 생성 #
def make_offsprings(generation):
ggap = 0.8 # 세대차
sorted_gen = sort_generation(generation) # 정렬된 해집단
n_parents = int(gen_size * (1.0 - ggap)) # 남겨놓을 부모 해의 개수
offsprings = sorted_gen[:n_parents] # 우수한 부모 해 그대로 남기기
roulette = make_roulette(sorted_gen) # 룰렛 생성
# 남은 수만큼 자식해 생성 후 대치
for i in range(gen_size - n_parents):
ca = selection(sorted_gen, roulette) # 부모해 선택 1
cb = selection(sorted_gen, roulette) # 부모해 선택 2
offspring = crossover(ca, cb) # 교차
offspring = mutation(offspring) # 변이
offsprings.append(offspring)
return offsprings
알고리즘 실행
알고리즘을 종료하는 기준은 해집단 내에서 목표 문자열이 완성된 해가 등장했을 때이다. 즉, 적합도 함수의 출력이 0인 해가 하나라도 발생하면 알고리즘을 종료한다. 초기 해집단의 생성부터 알고리즘 완료까지의 코드를 완성하자.
# get_best_chrono: 가장 우수한 해와 그 적합도 반환 #
def get_best_chrono(chronos):
fitnesses = [get_fitness(c) for c in chronos]
best_fitness = min(fitnesses)
best_idx = fitnesses.index(best_fitness)
return chronos[best_idx], best_fitness
# main 실행 코드 #
if __name__ == '__main__':
max_iter = 10000
best_fitness = 99999
iteration = 0
# 초기 해집단 생성
generation = make_random_generation()
# 종료 조건 만족(최적해 발견) 시까지 반복
while best_fitness > 0:
iteration += 1
best_chrono, best_fitness = get_best_chrono(generation)
if iteration % 10 == 0 or best_fitness == 0:
print('Gen', iteration, '---', 'Best:', best_chrono, 'fitness:', best_fitness)
generation = make_offsprings(generation)
print('Algorithm end!')
완성한 코드를 실행하면, 생각했던 대로 유전 알고리즘이 해집단을 목표 문자열로 수렴시키는 모습을 직접 확인할 수 있다. 초기 세대의 해집단에서는 매우 높은 적합도 값을 가지며 형체를 알 수 없는 해들이 등장하지만, 정답 해로의 수렴이 가까워질수록 적합도 값이 떨어지면서 목표 문자열과 비슷하게 변하는 것을 관찰할 수 있다.
Gen 10 --- Best: {fkkowb"oMÁNQ^m;´AH --- fitness: 789
Gen 20 --- Best: :Mskojb"dXshpMfJ¬+9cZr --- fitness: 394
Gen 30 --- Best: Hfkkowb"^du]shpMf^m;hpZr --- fitness: 231
Gen 40 --- Best: Hfkkojb"^du]shpMf^mhpZr --- fitness: 208
Gen 50 --- Best: Hfkkojb"Edu]shpRf^mhpZl --- fitness: 172
...
Gen 1770 --- Best: Genetic Algorithm is copl --- fitness: 1
Gen 1780 --- Best: Genetic Algorithm is copl --- fitness: 1
Gen 1790 --- Best: Genetic Algorithm is copl --- fitness: 1
Gen 1800 --- Best: Genetic Algorithm is copl --- fitness: 1
Gen 1803 --- Best: Genetic Algorithm is cool --- fitness: 0
유전 알고리즘은 시간이 무한하다면 무조건 수렴이 보장된다. 그러나 알고리즘이 확률의 영향을 크게 받기 때문에 수렴까지의 시간은 매 실행시마다 천차만별이다. 우리가 구현해본 예제는 매우 단순한 문제이기 때문에 알고리즘의 수렴이 빠르다. 그러나 문제가 어려워지고 해의 형태가 복잡해질수록, 해집단의 크기나 변이 확률 등 파라미터의 민감한 조절이 필요할 것이다. 이것이 유전 알고리즘을 실제 문제에 활용하기 어려운 이유다.
무한 원숭이 정리
컴퓨터 앞에 앉아서 키보드를 아무렇게나 두드리는 원숭이가 있다. 이 원숭이가 계속 키보드를 두드리다 보면 언젠가 이 책의 내용을 모두 완벽히 따라 칠 수 있을까? 상식적으로 말이 되지 않는 이야기로 들릴 것이다. 그러나 원숭이의 수를 무한하게 늘리고, 두들기는 시간을 무한대로 늘리면, 언젠가는 하나의 원숭이가 책을 완성할 수도 있을 것이다. 즉, 아주 낮은 확률이라도 발생의 가능성을 배제할 수 없음을 이야기하는 정리다. 유전 알고리즘도 이와 비슷하다. 수많은 해집단을 가지고 세대교체를 무한하게 반복하다 보면, 아무리 복잡한 문제라도 언젠가는 최적해를 찾아낼 수 있을 것이다. 그래서 유전 알고리즘의 수렴이 무조건 보장되는 것이다.
