“딥러닝 알아듣기” 시리즈는 딥러닝의 기초 지식을 저만의 방식으로 쉽게 풀어내는 시리즈입니다. 이번 챕터에서는 딥 러닝 모델의 설계와 학습 과정을 알아보고, 간단한 선형 회귀 모델을 직접 구현해봅니다.
이번 챕터에서 간단한 딥 러닝 모델을 직접 학습시켜볼 것이다. 앞으로 다루어 볼 그 어떤 딥 러닝 모델이라도, 학습의 전체적인 흐름은 이번 챕터와 동일하다. 학습의 각 과정에 대해 이론적으로 먼저 알아본 후, PyTorch 라이브러리를 사용해 같이 구현해보도록 하자.
3.2.1. 모델 학습 계획 세우기
문제 정의
이번 챕터에서 살펴볼 딥 러닝 모델은 선형 회귀(Linear Regression) 모델이다. 앞 장에서 선형 회귀 문제의 예시로 집 면적과 월세 가격 사이의 관계를 파악하는 문제를 제시했었다. 집의 면적을 입력으로 받아 예상되는 월세 가격을 출력하는 모델을 만드는 문제이다.
| 면적 | 월세 |
|---|---|
| 20 | 25 |
| 24 | 27 |
| 26 | 29 |
| 31 | 35 |
| 40 | 40 |
| 57 | 57 |
선형 회귀 모델은 집 면적과 월세 가격 사이의 관계처럼, 모델의 입력과 출력 사이의 선형 관계 를 찾는다. 집 면적 데이터를 입력으로 받아 예상 월세 가격을 출력하는 함수를 찾아내는 것이다. 집의 면적과 월세 가격은 대강의 선형 관계를 이루고 있기 때문에 이 문제를 선형 회귀로써 풀 수 있을 것이다. 다음 그림처럼 집 면적 데이터와 예상 월세 가격의 선형 함수 관계를 찾고자 하는 것이다. 빨간 직선이 우리가 찾아내고자 하는 함수이다.
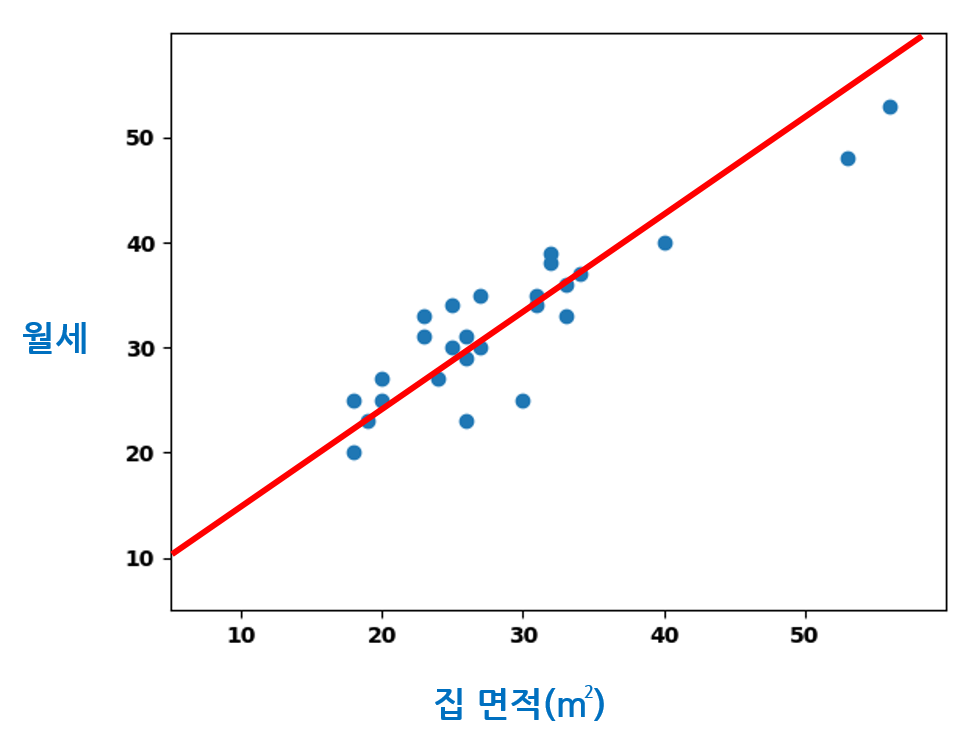
딥 러닝에서 이 함수 는 입력 데이터에 대한 각각의 가중치를 가지는 모델로써 구현된다. 모델에 어떠한 입력 데이터를 넣어 모든 가중치를 거쳐 연산했을 때, 모델의 출력 데이터와 실제 정답 데이터가 비슷할수록 모델이 입력과 출력 데이터 사이의 관계를 잘 이해하고 있다는 뜻이다.
딥 러닝 모델로써 이 함수를 찾아내려면, 각 입력 값이 출력 데이터에 미치는 영향을 결정하는 적절한 모델의 파라미터를 찾아야 한다. 모델의 파라미터를 찾는 과정을 모델을 최적화한다 고 한다. 모델을 학습한다 는 말과 같은 뜻이다. 모델을 최적화하기 위해서 수많은 입력 데이터와 정답 출력 데이터 쌍으로 이루어진 학습 데이터셋 을 충분히 준비한다. 이 데이터셋을 이용하여 모델이 각각의 입력 데이터에 대해 정답 데이터와 최대한 가까운 출력을 내놓도록 최적화하는 과정을 반복한다.
이제 대강 모델의 학습 과정이 어떻게 진행되는지 파악했으니, 집 면적 - 월세 가격 데이터셋의 준비부터 모델의 구현, 모델의 학습, 모델의 평가 과정까지 천천히 같이 구현해보도록 하자.
데이터셋 준비하기
집 면적과 월세 가격 쌍 데이터는 필자가 미리 준비해 놓은 것을 사용한다. 링크의 ‘monthly’ 디렉터리에서 다운받을 수 있다.
numpy 배열로 학습 데이터셋을 읽어들여보자. 파일 이름은 simple_monthly_train.csv 이다.
import numpy as np
import csv
train_data = np.genfromtxt('./simple_monthly_train.csv', delimiter=',', dtype=np.float32)
print(train_data)
np.genfromtxt 함수는 파일에서 값들을 delimiter의 문자로 끊어 읽어와서 numpy 배열에 적재한다. CSV 파일은 콤마(,) 기호로 값이 구분되어 있으므로 delimiter 인자로 콤마를 사용하였다. dtype=np.float32 인자는 읽어들인 데이터를 실수형으로 취급하도록 한다. 코드를 실행하면 아래와 같이 CSV 파일에서 데이터를 잘 읽어온 것을 볼 수 있다.
[[18. 20.]
[18. 25.],
...
[53. 48.]
[56. 53.]]
지금은 CSV 데이터를 모양 그대로 읽어온 것이므로 각각의 집 면적과 월세 데이터 쌍이 하나의 리스트로 묶여 있다. 데이터 사용의 편의를 위해서 집 면적 데이터와 월세 가격 데이터를 각각의 리스트로 묶자.
numpy 의 배열은 행렬 과 같이 사용할 수 있다. 배열로써 데이터를 읽었지만, train_data를 행렬로써 볼 수 있는 것이다. numpy가 지원하는 행렬 전치 연산을 통해 데이터의 형태를 바꾸자.
train_data = train_data.T
numpy 배열의 T 속성은 전치 행렬을 배열로써 돌려준다. 초기의 데이터를 전치하면 당연히 아래와 같이 우리가 생각했던 대로 만들어질 것이다.
[[18. 18. ... 53. 56.]
[20. 25. ... 48. 53.]]
matplotlib 라이브러리를 사용하면 읽어들인 데이터를 쉽게 시각화해볼 수 있다. scatter 함수를 이용해 <그림 1>과 같이 데이터의 분포를 그래프상에 그려볼 수 있다.
import numpy as np
import matplotlib.pyplot as plt
import csv
data = np.genfromtxt('./simple_monthly.csv', delimiter=',', dtype=np.float32)
plt.xlim(5, 60) # 그래프의 x축 범위를 [5, 60] 사이로 설정한다
plt.ylim(5, 60) # 그래프의 y축 범위를 [5, 60] 사이로 설정한다
plt.xticks(np.arange(10, 61, 10), fontweight='bold', fontsize=10) # 그래프의 x축 눈금 단위를 10으로 설정한다.
plt.yticks(np.arange(10, 61, 10), fontweight='bold', fontsize=10) # 그래프의 y축 눈금 단위를 10으로 설정한다.
plt.scatter(data.T[0], data.T[1]) # 집 면적은 x축, 월세 가격은 y축에 대응하여 그래프를 그린다.
plt.show() # 그래프를 띄워준다.
코드를 실행하면 아래와 같이 데이터의 분포를 2차원 평면상에 점으로 표현한 그림을 확인할 수 있다.

학습 데이터셋을 불러들인 과정과 동일하게 평가 데이터셋도 불러올 수 있다. 파일의 이름은 simple_monthly_test.csv 이다.
test_data = np.genfromtxt('./simple_monthly_test.csv', delimiter=',', dtype=np.float32)
평가 데이터셋은 학습 데이터셋과 내용이 전혀 겹치지 않는다. 학습시에는 보여주지 않고 모델의 평가에만 사용할 데이터셋이다.
텐서로 모델과 입출력 표현하기
데이터셋이 준비되었으니 우리가 최적화할 모델을 구현해보자. 입력과 출력 데이터 사이의 선형 관계 를 찾아야 하므로, 우리가 찾고자 하는 함수를 \(y = wx + b\) 꼴로 표현할 수 있을 것이다. 파이썬 코드로 이 함수를 표현하면 그것이 바로 우리가 학습해야 할 모델이 된다. PyTorch 라이브러리를 사용하여 모델을 구현해보자.
PyTorch로 딥 러닝 모델을 정의하기 위해서는 아래의 세 가지 형태를 같이 고려해야 한다.
- 입력 데이터의 형태
- 모델의 계산 구조
- 출력 데이터의 형태
PyTorch에서 데이터를 취급하는 기본적인 단위는 텐서(Tensor) 이다. PyTorch로 구현한 모델에 데이터를 입력할 때도 텐서로 입력해야 하며, 모델의 출력도 텐서로 이루어진다. 텐서는 행렬을 더욱 많은 차원으로 확장한 구조라고 생각하면 쉽다. 텐서의 엄밀한 정의는 생략하기로 하고, 행렬과 같이 많은 수를 정해진 차원과 모양으로 배열한 구조라고 생각하자. 2차원의 텐서는 행렬과 동일한 성질을 가진다.
이미 앞에서 신경망 모델을 행렬 연산으로 나타내는 방법에 대해 알아보았다. PyTorch에서 모델을 구현할 떄도 이 아이디어가 활용된다. 입력 데이터인 집 면적 데이터는 실수 값 하나이므로 (1 x 1) 모양의 텐서로써 나타낼 수 있다. 출력 데이터인 월세 가격 또한 (1 x 1) 모양의 텐서로 나타낼 수 있을 것이다. 따라서 가중치 파라미터 \(w\) 또한 (1 x 1) 모양의 텐서로 구현되어야 한다. 행렬곱 연산을 위해 가중치 행렬의 모양을 결정하는 과정을 그림으로 다시 떠올려보자.

입력 행렬의 열 수와 가중치 행렬의 행 수가 같아야 하고, 가중치 행렬의 열 수와 출력 행렬의 열 수가 같아야 한다. 그래야만 출력을 계산할 수 있다.
가중치와 같이 편향도 출력 데이터와 모양을 맞추어 구현해야 한다. 편향 행렬은 출력 데이터의 열 수에 맟추어 만들어주면 된다. 가중치 행렬의 각 열이 하나의 선형 함수를 구성하는 값들임을 생각해보면, 선형 함수들에 각각의 편향 값을 제공하기 위해서 편향 행렬을 다음 사진과 같이 구성해야 함을 알 수 있다.

우리의 입력 데이터와 출력 데이터가 각각 (1 x 1) 모양의 행렬이므로, 규칙에 따라 가중치 행렬과 편향 행렬의 모양은 각각 (1 x 1), (1 x 1)이 된다.
PyTorch에서 원소의 값이 0.5인 (1 x 1) 모양의 텐서는 아래와 같이 만들 수 있다. FloatTensor는 모든 요소가 실수형인 텐서를 만든다.
x = torch.FloatTensor([[0.5]])
입력 데이터를 정의했으니, 가중치와 편향을 가지는 모델 함수를 구현할 차례이다. 고맙게도 PyTorch는 정해진 모양의 가중치와 편향을 가지고 있는 선형 모델을 쉽게 구현할 수 있도록 지원한다. torch.nn.Linear가 바로 그것이다.
model = nn.Linear(1, 1)
nn.Linear(입력 텐서의 열 수, 출력 텐서의 열 수) 와 같이 선형 모델을 선언할 수 있다. 저 두 개의 값만 넘겨주면 PyTorch는 알아서 가중치 텐서와 편향 텐서의 모양을 결정할 수 있다. 위와 같이 모델을 선언해놓으면 PyTorch가 가중치와 편향 텐서의 모든 원소를 특정한 값으로 설정한다. 이 과정을 파라미터의 초기화(Initialization) 라고 한다. 초기화의 방법을 따로 정해주지 않으면 PyTorch가 설정한 초기화 방법으로 자동 초기화된다.
학습할 모델을 정의했으니, 입출력 데이터 설정에 대해 한 발짝 더 나아가보자. 방금 전 모델의 입력을 정의할 때 단 하나의 값만을 가지는 (1 x 1) 모양의 텐서로 정의했다. 아래와 같은 모양으로 모델이 정의되어 있을 것이다.

그러나 하나의 값만을 모델에 입력할 수 있는 (1 x 1) 모양의 입력 텐서로 모델을 최적화하는 과정은 매우 비효율적이다. 조금 후에 이야기하겠지만, 모델의 손실을 계산하는 데에도 부정적인 영향을 미친다.
입력 텐서의 크기를 키워서 여러 개의 입력 데이터에 대해 여러 개의 출력을 동시에 계산할 수 있도록 바꿔 보자. 가중치와 편향 텐서를 그대로 놓고 입력 텐서의 모양만 바꿈으로써 여러 개의 입력 데이터에 대해 출력 값을 동시에 계산하도록 만들 수 있다.
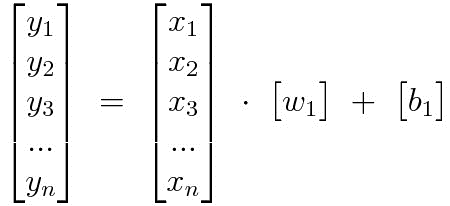
여러 개의 입력 데이터를 텐서에 쌓아 넣음으로써 동시에 계산하는 것이다. 입력 데이터의 행 수를 늘린 것이기 때문에 가중치 텐서와 편향 텐서의 모양과는 상관이 없다. 여러 입력 데이터에 대한 모델의 출력을 한 번의 행렬곱으로 계산해낼 수 있으니 계산상의 큰 이득을 볼 수 있다. 앞으로 모델을 최적화할 때, 대부분의 경우에는 이와 같이 여러 개의 데이터를 쌓아서 동시에 모델에 입력할 것이다.
오차의 설정과 손실 함수 구현
이제 본격적으로 모델이 어떻게 데이터로부터 학습할 수 있을지 방법을 생각해보자.
고등학생 때 시험공부를 했던 기억을 떠올려보면, 먼저 주어진 문제를 쭉 풀어본 후 틀린 문제에 대해서 다시 복습을 반복하는 방식으로 많이들 공부했을 것이다. 지도 학습을 하는 딥 러닝 모델의 학습도 똑같은 과정을 반복하며 학습한다. 학습 데이터셋을 모델에 입력하고, 입력된 데이터에 대한 출력을 만들어내도록 한다. 모델이 내놓은 출력과 학습 데이터셋에 표기된 정답의 차이가 얼마나 큰 지 확인한 후, 그 차이를 줄이기 위한 방향으로 모델의 파라미터들을 갱신해주면 된다. 더 이상 정답과의 차이를 줄이기 힘들 때까지 반복하면 그 때의 모델이 학습 데이터에 가장 잘 최적화된 모델일 것이다.
그렇다면 모델 학습시에 한 번의 반복은 아래와 같이 순차적으로 이루어져야 한다.
- 학습 데이터셋에서 입력 데이터를 가져와 모델에 입력한다.
- 모델의 출력과 정답 데이터의 차이가 얼마나 크게 나는지 확인한다.
- 모델의 출력이 정답 데이터와 가까워질 수 있는 방향으로 모델의 파라미터를 갱신한다.
모델의 최적화 과정에서 핵심은 두 번째 과정이다. 모델의 출력과 정답 사이의 차이를 손실(Loss) 이라고 하고, 손실을 계산하는 함수를 손실 함수(Loss Function) 라고 한다. 손실을 문제 상황과 데이터의 특성에 맞게 합리적으로 계산해야 모델의 파라미터를 옳은 방향으로 갱신할 수 있다. 그래서 어떤 딥 러닝 모델을 학습하더라도 손실 함수의 합리적인 정의는 필수이다. 데이터셋과 문제 상황에 가장 적절한 손실을 계산할 수 있는 방법이 필요하다.
선형 회귀 모델에서 손실의 계산에는 평균 제곱 오차 가 널리 쓰인다. 영어로는 Mean Squared Error(MSE) 라고 부른다. 명칭 그대로 각 데이터의 오차의 제곱의 평균 을 모델의 손실로써 계산하는 방법이다.
모델 학습 중 특정 시점에서의 손실을 계산한다고 생각해보자. 현재 모델의 가중치와 편향 파라미터의 영향으로, 입력 데이터에 따른 모델의 출력이 다음과 같이 선형으로 나타날 것이다.
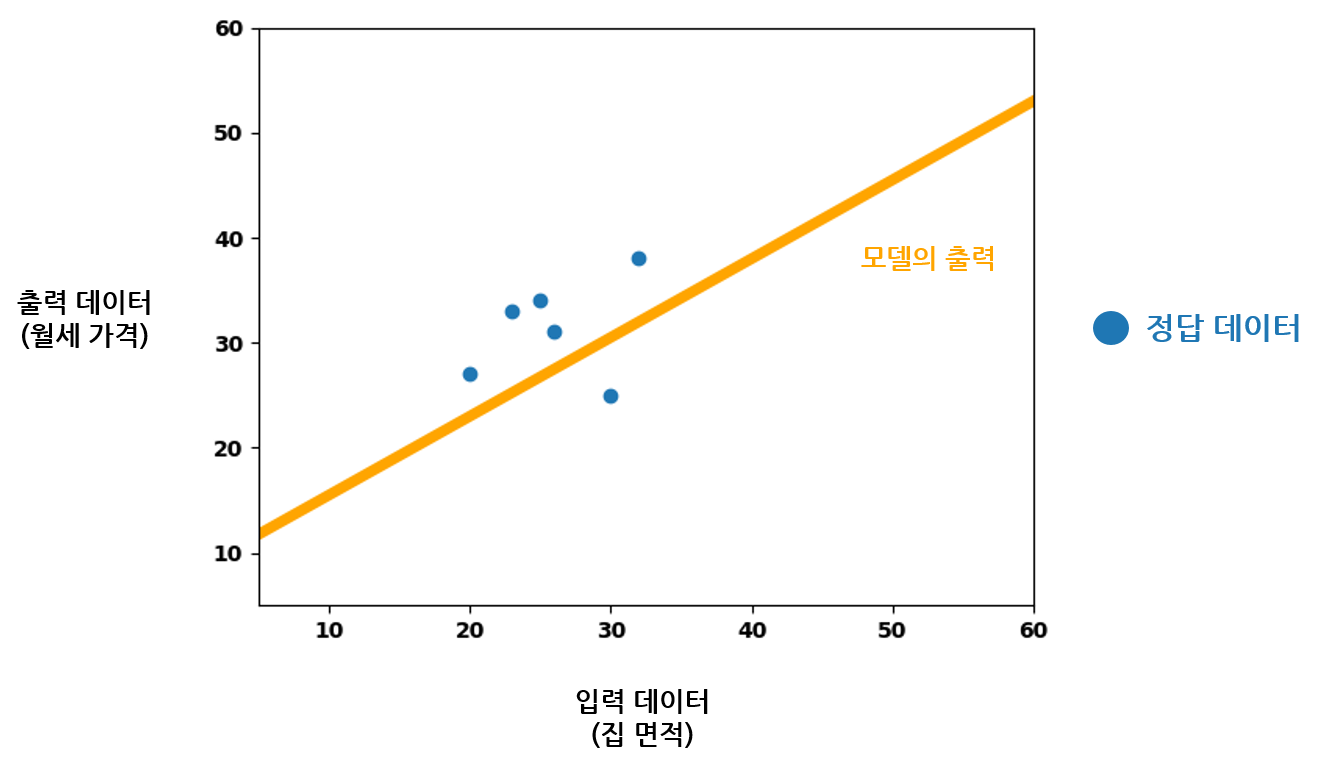
그래프의 가로축이 모델에 입력되는 집 면적 데이터이다. 선형 함수를 구현하는 모델이므로, 가능한 모든 입력 값에 대한 모델의 출력을 모으면 주황색 실선과 같이 나타난다. 모델이 가지는 오차(Error) 는, 위의 그래프에서 파란색 정답 데이터의 월세 가격과 주황색 모델 출력 데이터의 월세 가격 사이 차이를 이야기한다. 입력 값들이 동일할 때, 정답과 모델의 출력이 얼마나 크게 차이나는지를 이야기하는 것이다. 각각의 입력 값에 대한 오차를 빨간 실선으로 나타내면 다음 그림처럼 보여진다.
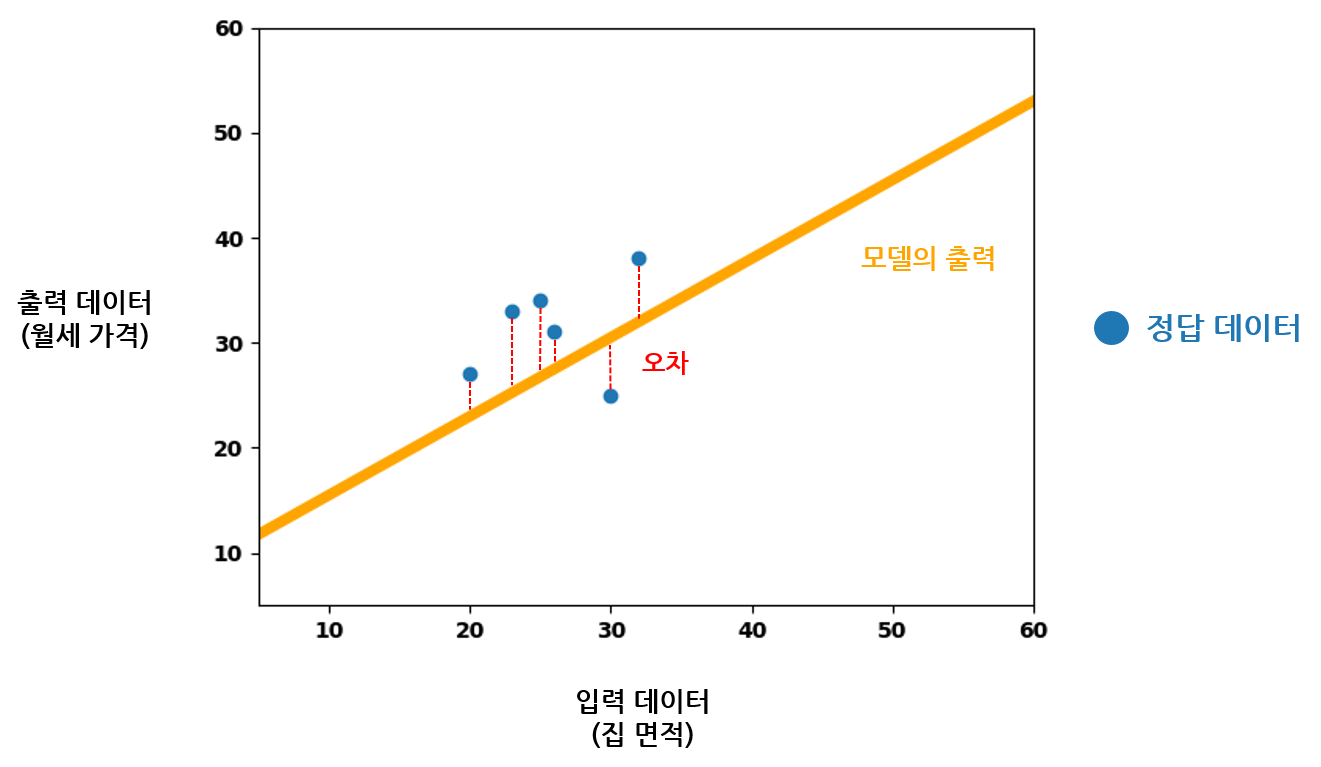
원래 구하고자 했던 것은 데이터 각각의 오차보다는 모델 학습의 한 반복에서 오차의 총합이다. 그러므로 모든 입력 데이터에 대한 오차의 총합을 구해서 모델의 손실로 사용하는 것이 적절해 보인다.
한 번의 반복에서 구해지는 모델의 평균 제곱 오차를 수식으로 나타내보자. 입력 데이터 \(x\)가 \(n\)개만큼 모델에 동시 입력된다. 각각의 입력 데이터에 대한 정답 데이터 \(y\) 또한 \(n\)개 존재할 때, 이번 반복에 입력된 데이터에 대한 모델의 오차 \(L(x, y)\)는 아래와 같이 정의된다.
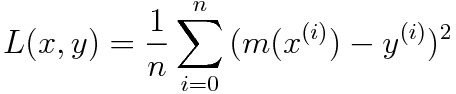
수식은 어렵지 않다. 모델의 출력 데이터 \(n\)개와 정답 데이터 \(n\)개의 오차를 각각 구해서 제곱하고, 모두 더해서 입력 데이터 개수로 평균을 내는 것이다. 이렇게 하면 여러 출력에 대한 오차의 평균 을 구해낼 수 있다. 모델의 출력과 정답 데이터의 차를 제곱하는 이유는 오차가 음수로 계산되는 상황을 방지하기 위해서이다. 정답 데이터와 출력의 상대적인 위치에 상관없이, 오차는 무조건 정답과의 거리 차이를 나타내는 양수 값이어야 한다. 오차 값에 음수가 허용되면 평균으로 정확한 모델의 오차를 구할 수 없다.
파이썬으로 다음과 같이 오차 함수를 구현할 수 있다.
# pred, y가 각각 모델의 출력 리스트, 정답 데이터 리스트라고 가정한다.
def mse(pred, y):
n = len(pred)
error = 0
for i in range(n):
error += (pred[i] - y[i]) ** 2 # 오차의 제곱을 계산한다.
return (float(error) / float(n)) # 오차의 평균을 반환한다.
하지만 PyTorch는 이미 평균 제곱 오차를 계산하기 위한 함수를 제공한다. torch.nn.MSELoss() 객체를 사용하면 된다. 계산 방식 또한 위에서 우리가 직접 구현한 평균 제곱 오차와 동일하다. 아래와 같은 방식으로 평균 제곱 오차 손실 함수를 정의하고 이용할 수 있다.
import torch.nn as nn # torch.nn 패키지의 import가 필요하다
lossf = nn.MSELoss() # lossf를 MSE Loss 계산 함수로 정의한다.
...
loss = lossf(prediction, y_label) # 모델의 출력과 정답 레이블을 인자로 손실을 계산한다.
이로써 모델을 학습하는 기준이 될 손실 함수의 정의도 완료하였다. 손실 함수를 어떻게 디자인하는지에 따라 딥 러닝 모델의 학습 결과가 크게 달라질 수 있으니, 문제 상황과 데이터의 특성에 맞는 적절한 손실 함수의 디자인에 신경써야 한다. 실제로 딥 러닝 모델을 만들고 학습시킬 때 가장 민감하면서도 어려운 부분이 손실 함수의 정의인 이유다.
경사 하강법으로 모델 최적화하기
학습 데이터셋을 불러왔고 손실도 정의했으니, 이제 데이터로부터 모델을 학습할 차례다.
천천히 생각해보자. 모델에 입력되는 데이터가 동일하다고 가정했을 때, 모델의 파라미터가 바뀌면 모델의 출력이 바뀐다. 그리고 모델의 출력이 바뀌면 손실도 같이 변화한다. 그리고 모델을 최적화시키는 과정은 손실을 줄이는 방향으로 파라미터를 갱신하는 과정 이다. 따라서 모델의 손실 값을 보고 파라미터를 어떻게 갱신할 것인지 결정하는 알고리즘이 필요하다.
파라미터의 갱신 방법을 찾기 위해서, 먼저 파라미터와 손실 사이의 관계를 파악해야 한다. 파라미터의 값에 따른 손실의 변화를 예상할 수 있어야 한다는 것이다.
먼저, 모델의 가중치 파라미터 변화에 따른 손실의 변화를 그래프로 그려 보자. 0.6에서 1.6 사이의 값으로 해당 가중치의 값을 변경해가면서, 각 지점에서 학습 데이터셋에 대한 모델의 손실을 계산해 그래프로 나타낸다. 이 때 모델의 입력과 편향 파라미터는 특정 값으로 고정해놓고 계산한다. 손실의 변화에 있어 변인은 가중치 하나여야 하기 때문이다. 이렇게 그린 그래프는 다음과 같이 가중치 파라미터와 손실 사이의 관계를 하나의 곡선으로 나타낼 것이다. 예시를 들기 위해 임의로 그린 그래프이므로 우리의 모델에서는 다른 그래프가 그려질 수 있다.
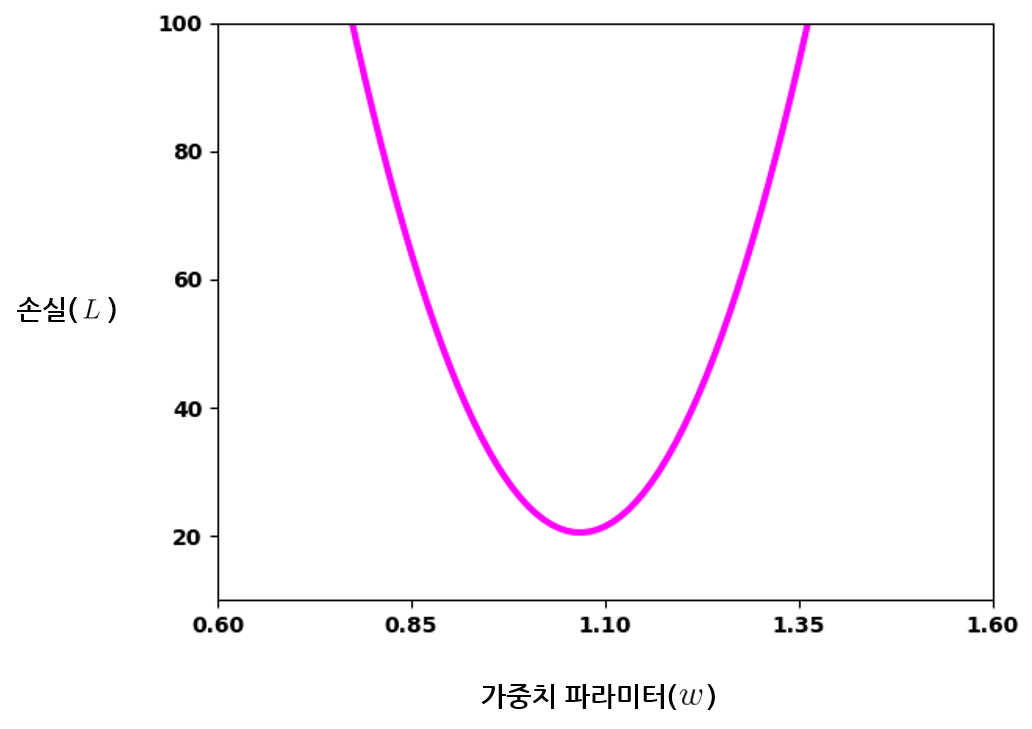
그래프를 보면 가중치 값이 약 1.05에 가까운 지점에서 손실이 최소가 되는 것으로 보인다. 모든 파라미터 값들 중 손실이 가장 최소가 되는 점을 손실 함수의 전역 최저점(Global Optima) 이라고 한다. 위 그래프에서 손실이 전역 최저점에 위치하는 가중치 값이 모델의 최적화 목표이다. 모델 학습을 시작할 때의 가중치 초깃값에 상관없이, 결국 손실이 최소가 되는 가중치 값으로 갱신되어야 한다.
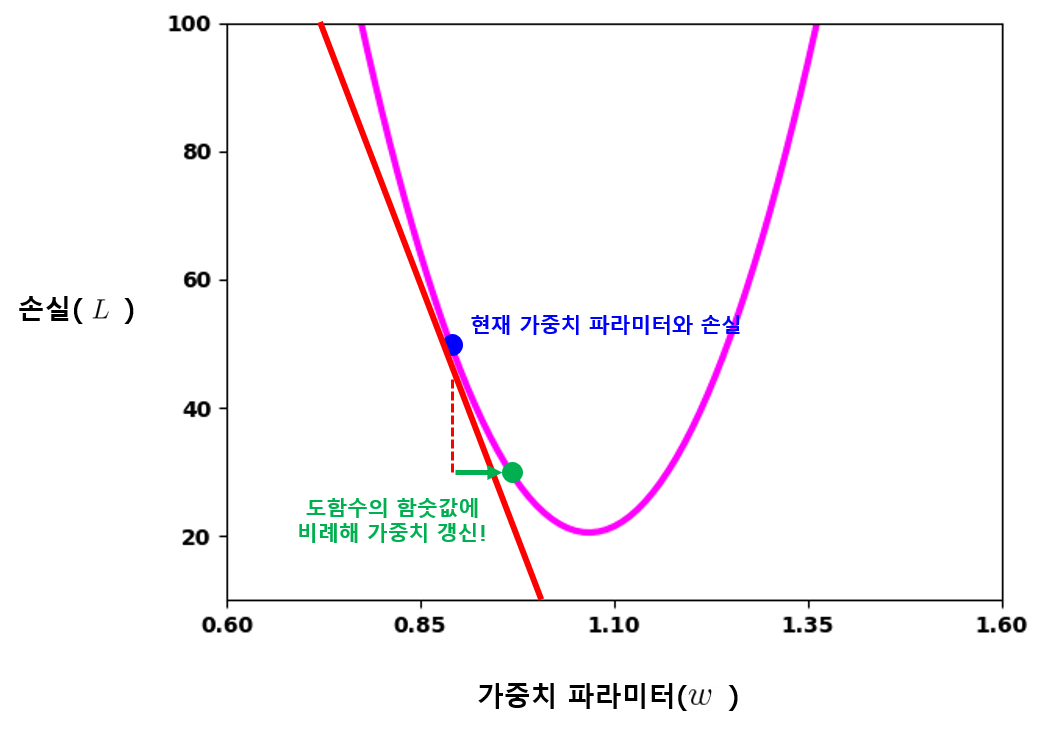
모델의 학습이 진행되는 도중에, 가중치의 값이 아래 그래프에서처럼 특정한 위치에 있다고 가정해보자.
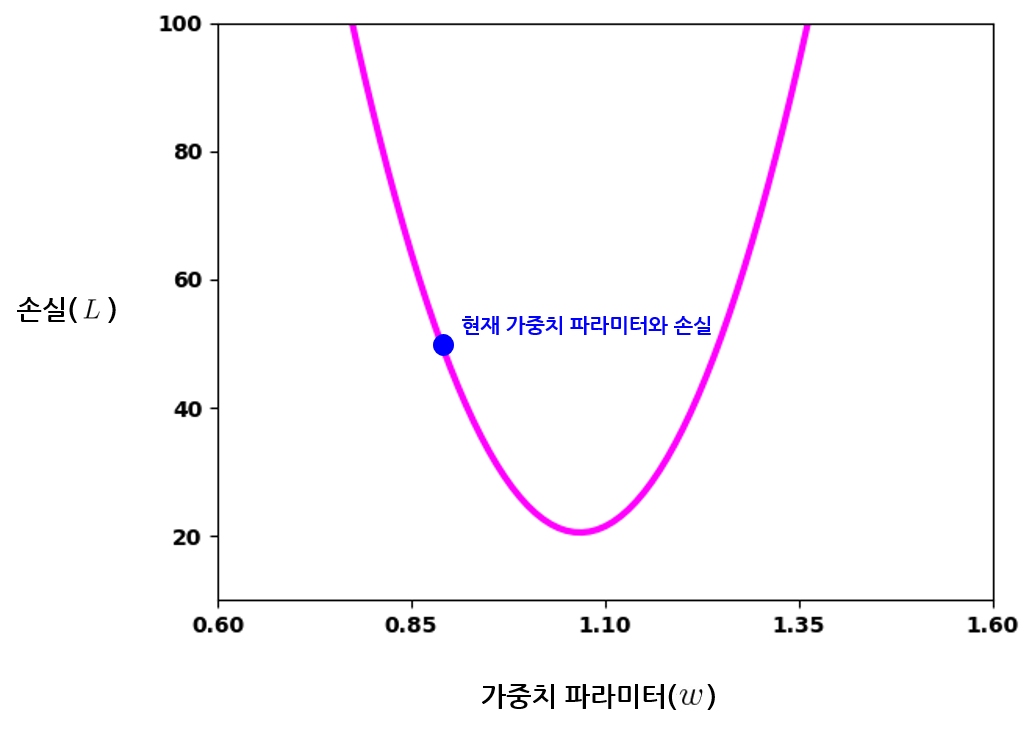
현재 가중치의 값이 약 0.9로 파란 점 위치에 있다. 현재 가중치 값에 따른 손실은 약 50으로 계산된다. 손실을 줄이는 방향으로 가중치 \(w\)를 업데이트하려면, 값을 더 키워 1.1에 가까워지도록 갱신해야 한다.
그럼 가중치 값의 갱신 방향과 정도를 어떻게 결정할 수 있을까? 앞 그래프의 시점에서 방법을 생각해보자. 그래프를 살펴보면, 가중치 값의 위치와 손실의 변화에서 중요한 특징을 찾아낼 수 있다. 가중치 \(w\)의 값이 약 1.05가 되어 손실이 최저가 되는 지점을 기준으로, 가중치 값이 양쪽으로 멀어질수록 손실이 증가하는 양상을 파악할 수수 있다. 더 일반화해보면, 특정 지점에서 가중치 값을 갱신했을 때 손실이 어떻게 변할지 그래프상에서 예측할 수 있다. 그래프의 파란 점에서 가중치 값을 조금이라도 키우면 손실이 작아지고, 가중치 값을 조금이라도 줄이면 손실이 커지는 것을 예측할 수 있듯이 말이다.
수학적으로 보면, 특정한 값에서부터 함수의 입력이 조금씩 변화함에 따른 함숫값의 변화 양상을 확인하는 일과 같다. 다행히 수학은 이 문제에 대해 기가 막힌 방법을 제공해주는데, 현재 위치에서 함수의 그래디언트(Gradient, 기울기) 를 구해보는 방법이다.
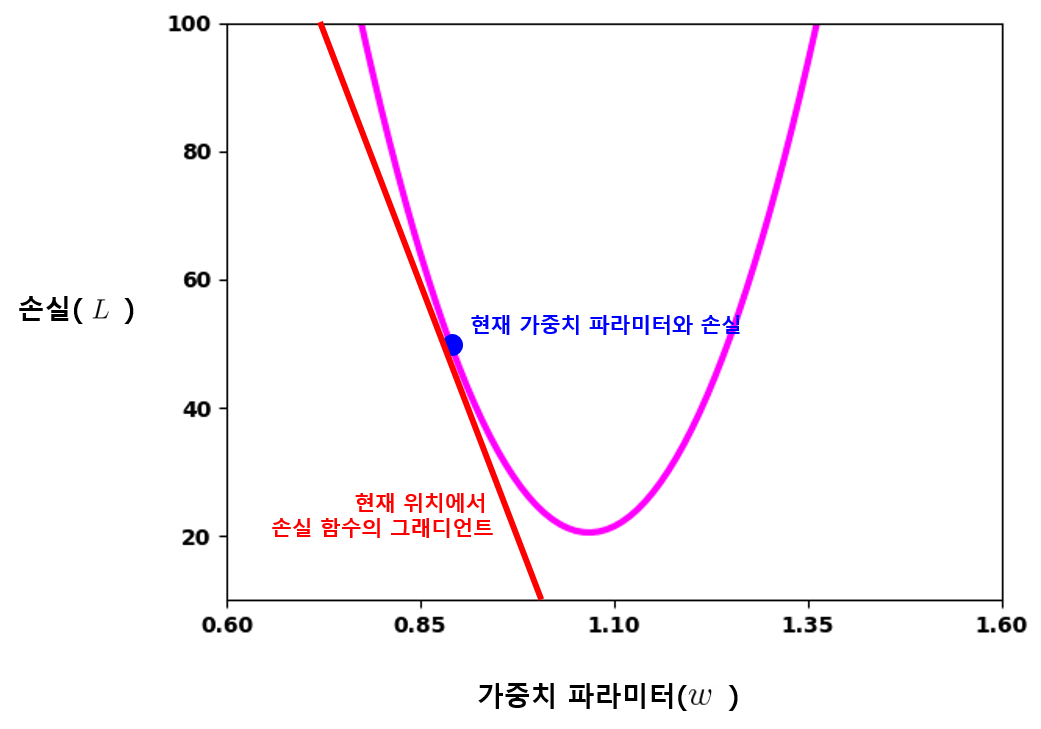
파란 점 위치에서의 빨간 그래디언트 직선이 우리에게 답을 알려주고 있다. 파란 점에서의 그래디언트 방향이 \(w\)가 커질수록 손실이 작아진다고 이야기한다. 특정 지점에서 함수의 그래디언트를 구하는 방법을 고등학교 시절에 미분(Differential) 이라는 이름으로 배웠다. 미분으로 얻어낸 함수를 도함수(Derivative) 라고 했다. 위의 손실 함수를 가중치 \(w\)에 대해 미분하면 손실 함수의 도함수가 나오고, 도함수에 다시 \(w\)를 대입해보면 현재 위치에서의 그래디언트 값을 구할 수 있다. 가중치 값을 어느 방향으로 갱신해야될지 알아낸 것이다. 현재 위치에서의 그래디언트가 하강하는 직선이라면 그래디언트 값이 음수일 것이고, 상승하는 직선이라면 그래디언트 값이 양수일 것이다. 그렇다는 것은 그래디언트 값에 비례하여 현재 가중치 값을 줄여 주면 , 손실이 줄어들도록 가중치 값을 갱신할 수 있다는 이야기다. 이 과정을 수식으로 나타내면 아래와 같다.
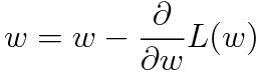
드디어 가중치 값을 갱신할 방법이 생겼으나, 한 가지 문제점이 있다. 가중치 값에서 그래디언트 값을 그대로 빼면 가중치 값이 너무 큰 폭으로 변하게 된다. 손실 값과 가중치 값의 단위 자체가 다르기 때문이다. 앞의 그래프만 봐도 확실히 알 수 있는데, 가중치 값이 0.85에서 0.95로 0.1만 증가해도 손실 값은 약 57에서 38로 크게 떨어진다. 이 말은 즉, 각 지점에서의 그래디언트 값도 그만큼 크다는 이야기이다. 이렇게 큰 값을 가중치 \(w\)에서 바로 빼 버리면 가중치의 절댓값이 폭발적으로 늘어날 것이다.
그래서 학습률(Learning Late) 을 도입한다. 정해진 학습률을 그래디언트 값에 곱해서, 그래디언트 값에 따라 가중치 값이 갱신되는 절대량을 조절한다. 우리 문제에서는 0.001 정도가 적당하다. 가중치 파라미터가 적당히 갱신될 수 있도록 그래디언트 값의 크기를 맞춰주는 것이다. 학습률 \(\eta\)를 적용한 수식은 아래와 같이 변경된다.
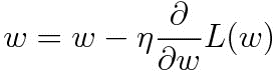
앞에서 가중치 파라미터를 갱신한 것처럼, 어떠한 모델의 파라미터에 대해 이 과정을 반복하면서 파라미터를 갱신하는 방법을 경사 하강법(Gradient Descent) 이라고 한다. 현재 파라미터에 따라 계산된 손실 함수의 그래디언트를 바탕으로, 손실이 줄어드는 방향으로 내려가면서 파라미터를 갱신하는 과정이기 때문이다. 손실의 하락은 곧 모델의 최적화를 의미하므로, 경사 하강법이 딥 러닝 모델 최적화의 핵심임을 알 수 있다.
모델의 편향 파라미터 \(b\) 또한 똑같이 경사 하강법을 사용해 최적화할 수 있다.
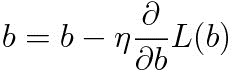
확률적 경사하강법
경사하강법은 딥 러닝 모델의 최적화를 위한 확실하면서도 직관적인 방법이다. 그러나 실제 상황에 사용되는 큰 모델의 최적화에 적용하기에는 아직 무리가 있다.
경사하강법은 모델의 손실과 그에 따른 그래디언트 값을 바탕으로 동작한다. 학습 데이터셋 전체에 대해 손실을 줄이는 방향으로 파라미터를 갱신하려면, 당연히 학습 데이터셋 전체에 대한 손실을 먼저 구해야 한다. 학습 데이터셋의 양이 적으면 어렵지 않겠지만, 학습 데이터셋의 양이 수백만개, 수천만개로 많아진다면 손실을 구하는 것 자체가 버거운 일이 된다.
그래서 등장한 대안이 확률적 경사하강법(Stochastic Gradient Descent, SGD) 이다. 확률적 경사하강법은 학습 데이터셋에서 무작위로 하나 의 데이터를 선별해서, 모델의 손실을 구하고 파라미터를 갱신한다. 전체 데이터셋에 대한 손실을 한꺼번에 계산하지 않으니 계산량이 크게 줄어든다. 따라서 파라미터의 갱신이 매우 빨라질 것이다.
그러나 확률적 경사하강법으로 하나의 데이터만을 이용해 파라미터를 갱신하면, 각 입력 데이터마다 모델의 손실 차이가 너무 크다 는 문제가 발생한다. 전체 학습 데이터셋에 대한 평균적인 손실을 바탕으로 최적화하기 위해서 경사하강법을 사용했는데, 각 데이터에 대한 손실을 따로 구하면 각각 손실의 편차가 크므로 당연히 일관적으로 파라미터를 갱신할 수 없다.
그래서 등장한 방법이 미니 배치 경사하강법(Mini-Batch Gradient Descent) 이다. SGD가 단 한개의 데이터만을 사용하는 것이 문제라고 했다. 또한 전체 데이터셋을 한번에 이용하는 것은 사실상 불가능하다. 그래서 둘의 절충안으로, 무작위로 학습 데이터셋에서 \(n\)개의 데이터를 선별해 묶어서 사용한다. 이렇게 학습 데이터에서 무작위로 일부를 추출한 묶음을 배치(Batch) 라고 하고, 작은 배치를 만들어 사용한다는 뜻으로 미니 배치(Mini-batch) 로 부른다. 이 때 \(n\)을 배치 크기(Batch Size) 라고 하며, 배치 경사하강법의 최적화 성능의 중요한 열쇠다.
미니 배치를 사용하면 SGD의 빠른 파라미터 갱신 속도를 어느 정도 가져오면서, 비교적 많은 데이터에 대한 평균 손실을 계산하므로 기존 경사하강법의 학습 능력도 어느 정도 기대할 수 있다. 배치 크기가 커질수록 더욱 정확한 파라미터의 갱신이 가능하고, 배치의 크기가 작아질수록 학습 반복의 속도가 더 빨라질 것이기 때문이다. 그래서 적절한 배치 크기의 선정이 매우 중요하다.
위에서 이미 여러 학습 데이터를 하나의 텐서로 쌓아서 한번에 모델에 입력하는 방법을 살펴보았는데, 이것이 미니 배치 를 만드는 과정이었던 것이다. 미니 배치를 만들어 모델에 입력하면 GPU의 병렬 연산을 활용해 모델이 여러 개의 데이터를 더 효율적으로 처리할 수 있다. 그래서 딥 러닝 모델의 학습 반복은 보통 배치 단위 학습 데이터로 이루어진다.
확률적 경사하강법과 미니 배치 경사하강법을 나눠서 이야기했지만, 대부분의 경우 둘은 모두 미니 배치 경사하강법을 의미한다. 확률적 경사하강법 또한 데이터의 갯수가 한 개인 미니 배치를 사용하는 것으로 볼 수 있기 때문이다. 그리고 사실상 반복마다 한 개의 데이터만을 사용하는 경우는 없다. 모델에게 적당한 크기의 미니 배치를 연속해서 보여줌으로써 전체 학습 데이터셋의 경향을 이해해야 한다. 그러나 학습 반복마다 하나씩의 데이터만 보여주면, 반복마다 비슷한 경향성을 찾을 수가 없어 학습에 실패할 확률이 크다. 앞으로 확률적 경사하강법을 이야기하면 미니 배치를 활용한 경사하강법으로 이해하면 된다.
확률적 경사하강법을 사용하면 아무래도 학습 초반에는 기존 경사하강법보다 최적점을 찾는 과정이 더딜 수 있다. 그러나 모델에 한 번 입력되는 학습 데이터의 양이 적어지므로, 같은 시간 안에 파라미터 갱신을 더 많이 반복해서 이 단점을 상쇄시킬 수 있다. 그러므로 확률적 경사하강법을 적용해서 우리의 모델을 최적화하도록 하자.
PyTorch에서 확률적 경사하강법의 사용
확률적 경사하강법과 같이 모델의 손실을 바탕으로 파라미터를 갱신하는 방법을 최적화 기법 이라고 한다. PyTorch의 torch.optim 모듈에 다양한 최적화 기법이 구현되어 있으며, SGD 객체를 사용해서 확률적 경사하강법을 구현할 수 있다. 다음과 같이 선언한다.
optimizer = torch.optim.SGD(model.parameters(), lr=0.0005)
미니 배치를 모델에 입력해 손실을 계산한 후, optimizer를 이용해 확률적 경사하강법을 구현한다. 첫 번째 인자로 모델의 모든 파라미터 리스트를 넘겨주고, 두 번째 인자 lr로 학습률을 설정한다. optimizer는 알아서 모델의 모든 파라미터를 학습률에 따라 갱신한다.
3.2.2. 모델 학습하기
이로써 모델의 학습을 위한 이론적인 배경을 모두 살펴보았다. 이제 PyTorch를 사용해서 모델 학습의 모든 과정을 직접 구현해보자.
데이터셋 불러오기
먼저 학습 데이터셋을 불러온 후, 미니 배치의 크기를 설정한다.
import numpy as np
# 학습 데이터셋이 담긴 CSV 파일을 읽는다.
data = np.genfromtxt('./monthly_data.csv', delimiter=',', dtype=np.float32)
data = data.T # 데이터를 행렬 전치하여 사용하기 좋은 모양으로 변환한다.
data_x = list(np.expand_dims(data[0], axis=1)) # 입력 데이터 리스트
data_y = list(np.expand_dims(data[1], axis=1)) # 정답 데이터 리스트
data_size = len(data_x) # 데이터의 총 개수
batch_size = int(data_size / 2) # 미니 배치의 크기
학습 데이터셋이 담긴 CSV 파일을 읽어서 입력 데이터와 정답 데이터의 리스트를 각각 구성한다. numpy.expand_dims 함수는 numpy 배열의 차원을 한 차원 증가시켜준다. (batch_size x 1) 크기의 입력 데이터와 정답 데이터를 만들기 위해 데이터 리스트의 모양 자체를 바꾸는 것이다. 위 코드와 같이 expand_dims 함수를 사용하면 다음과 같이 리스트의 형태가 변화한다.
[1, 2, 3, 4, 5]
[[1], [2], [3], [4], [5]]
모델과 최적화 과정 구현하기
다음으로, 최적화할 모델을 정의한다. (1 x 1) 모양의 가중치 텐서와 (1 x 1) 모양의 편향 텐서를 가지는 선형 모델을 정의한다.
model = nn.Linear(1, 1) # bias=True 기본 설정된다.
모델을 정의했으니, 모델 최적화의 기준이 되는 손실 함수와 최적화 기법을 각각 정의한다. 손실 함수로 MSE를 사용하고, 최적화 기법으로는 학습률이 0.0005인 확률적 경사하강법을 사용한다.
lf = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.0005)
학습 반복의 횟수를 설정하고, 학습 도중 손실 값을 얼마나 자주 출력할 것인지 설정한다. show_freq만큼 최적화를 반복한 후, 그 사이에서 계산된 모든 손실 값을 평균내어 학습 상황을 확인할 것이다.
max_iteration = 100000 # 최적화 반복 횟수
show_freq = 100 # 평균 손실을 확인할 반복 횟수
loss_sum = 0.0 # 평균 손실 계산을 위함
학습을 위한 모든 사전 준비가 끝났으니 본격적으로 학습 반복을 구현하자.
for i in range(max_iteration):
# 입력 데이터와 정답 데이터 리스트에서 무작위로 배치 크기만큼 추출한다.
zipped_data = list(zip(data_x, data_y))
train_x, train_y = zip(*random.sample(zipped_data, batch_size))
x_tensor = torch.FloatTensor(train_x) # (batch_size, 1) 크기 입력 데이터 텐서를 만든다.
y_tensor = torch.FloatTensor(train_y) # (batch_size, 1) 크기 정답 데이터 텐서를 만든다.
prediction = model(x_tensor) # 모델에 데이터를 입력해 출력 텐서를 구한다.
loss = lf(prediction, y_tensor) # 출력 텐서와 정답 텐서 사이의 손실을 MSE로 구한다.
# 구한 손실 값을 바탕으로 경사 하강법을 한번 실행한다.
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 일정 횟수마다 평균 손실을 구해 출력해준다.
loss_sum += loss.item()
if i % show_freq == 0:
print('Iteration {} --- Loss: {}'.format(i, loss_sum / show_freq))
loss_sum = 0.0
학습 데이터셋에서 무작위로 배치 크기만큼 추출해서 입력 데이터와 정답 데이터 텐서를 각각 생성한다. 모델에 입력 텐서를 넣어 출력 텐서를 구한 후, 정답 텐서와의 MSE를 계산해서 손실로 사용한다. loss.backward 함수와 optimizer.step 함수를 차례대로 실행하면 경사 하강법으로 모델의 모든 파라미터가 한 번 갱신된다. 두 함수가 파라미터를 갱신하는 자세한 원리는 이후 챕터에서 같이 살펴볼 것이다.
모델 학습하기
전체 코드는 monthly_prediction.py 파일에서 확인해볼 수 있다. 파이썬 파일을 실행하면 학습이 진행되는 모습을 직접 확인할 수 있다. 반복 횟수가 늘어날수록 아래처럼 평균 손실이 계속 하락할 것이다. 드디어 우리의 모델이 데이터로부터 학습하고 있다는 증거이다.
Iteration 0 --- Loss: 1529.136962890625
Iteration 100 --- Loss: 21.503562927246094
...
Iteration 9900 --- Loss: 10.846819877624512
Iteration 10000 --- Loss: 10.824003219604492
...
Iteration 98600 --- Loss: 10.518432078361512
Iteration 98700 --- Loss: 9.989933947324753
...
반복의 진행에 따른 손실의 하락을 그래프로 그려서 확인해볼 수도 있다. 많은 경우 다음과 같이 그래프로 손실의 경향을 확인한다.
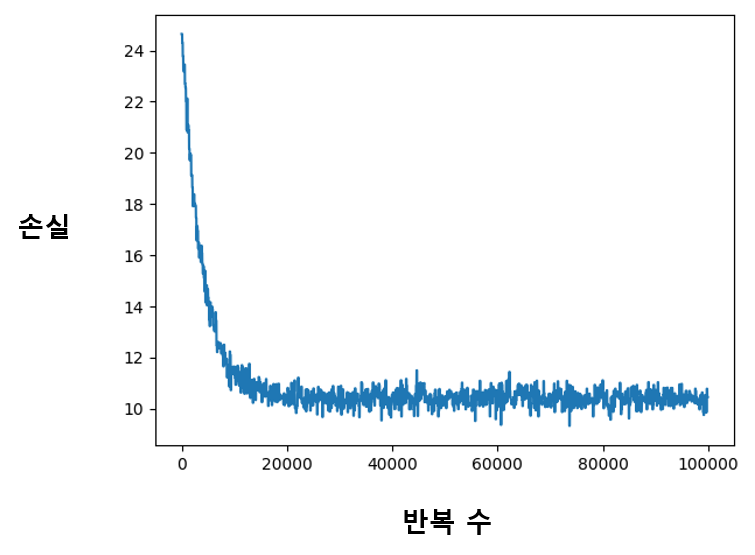
3.2.3. 모델 학습 결과 확인하기
드디어 월세 가격 예측 모델의 학습을 완료했다. 이제 평가 데이터셋을 이용해 학습이 얼마나 잘 되었는지 확인해보자.
모델의 성능을 판단하는 기준을 평가 지표(Metric) 라고 한다. 문제 상황과 모델에 맞는 적절한 평가 지표를 설정해야 모델의 성능을 정확히 판단할 수 있다. 모델의 평가 지표는 정의하기 나름이다. 필자는 모델의 학습시와 비슷하게, 정답 데이터와 모델 출력 간 오차의 절대량을 보는 것이 평가 지표로써 적절하다고 생각했다. 더 나은 평가 지표가 떠오른다면 그것으로 성능을 평가해도 무방하다.
결정한 평가 지표인 평균 오차를 계산하는 함수를 아래와 같이 구현할 수 있다.
# 모델의 출력과 정답 데이터 간의 평균 오차를 계산한다.
def avg_error(predict, answers):
data_count = len(predict)
error = 0.0
for i in range(data_count):
error += abs(predict[i][0] - answers[i][0]) # 오차의 절대량
return error / data_count # 평균 오차 계산
avg_error 함수는 평가 데이터셋의 배치를 모델에 입력해 출력 배치를 얻어낸다. 그 후 같은 갯수인 정답 데이터와의 오차를 각각 계산해서 평균을 반환한다.
실제로 평가 데이터셋을 불러와서 모델이 얼마나 잘 학습되었는지 확인해보자. 모델의 학습을 완료한 후, 아래와 같이 평가 데이터셋에 대해 모델의 평가 지표를 계산할 수 있다. 평가 데이터셋의 크기가 크지 않으니, 전체를 한 번에 모델에 입력하고 평균 오차를 계산할 수 있다.
def test_model(model):
# 학습 데이터셋과 동일한 방법으로 평가 데이터셋을 불러온다.
data = np.genfromtxt('./monthly_data_test.csv', delimiter=',', dtype=np.float32)
data = data.T
data_x = list(np.expand_dims(data[0], axis=1))
data_y = list(np.expand_dims(data[1], axis=1))
# 전체 평가 데이터셋을 모델에 입력하여 출력 텐서를 구한다.
x_tensor = torch.FloatTensor(data_x)
y_tensor = torch.FloatTensor(data_y)
prediction = model(x_tensor)
# 출력 텐서와 정답 텐서의 평균 오차를 구한다.
# 평균 오차가 작을수록 모델의 성능이 좋은 것이다.
error = avg_error(prediction.data.numpy(), y_tensor.data.numpy())
print('Test Error :', error)
test_model 함수는 평가 데이터셋 전체를 불러와서 한꺼번에 모델에 입력하고, 출력과 정답 데이터간의 오차를 계산한다. 데이터를 불러오는 과정은 학습 때와 동일하다.
작성한 평가 함수를 바탕으로, 모델의 학습 반복을 1천번 수행했을 때와 10만번 수행했을 때 평균 오차의 차이를 확인해보자. 필자가 학습한 모델의 경우 1천 번 반복한 모델은 약 9.26 의 평균 오차를 가진 반면, 10만 번 반복한 모델은 6.81 의 평균 오차를 보였다. 학습을 많이 반복할수록 유의미하게 오차가 줄어드는 결과를 보인 것이다. 그만큼 데이터를 더욱 정확하게 이해하는 모델을 찾아냈다는 이야기이다.
학습이 완료된 모델의 가중치와 편향 파라미터를 이용해 직접 모델이 찾아낸 직선을 그려 보면, 학습 반복을 더 많이 수행한 모델이 더욱 정확한 직선을 찾아낸 모습을 확인할 수 있다.

모델의 학습 반복을 더 많이 수행할수록 모든 데이터에 대한 평균 오차가 줄어드는 방향으로 파라미터가 수렴 한다. 학습시에 평균 오차는 곧 모델의 손실이므로, 손실 함수에서 모델 파라미터의 전역 최적점을 찾아가는 것과 동일한 말이다.
앞의 결과에서 볼 수 있듯이, 딥 러닝 모델의 학습 목표는 최대한 많은 평가 데이터에 대한 성능을 골고루 높이는 것이다. 딥 러닝의 단어로 주어진 데이터셋에 대해 가장 일반화(Generalize) 된 모델을 찾아내는 것이라고 이야기한다. 최대한 많은 데이터에 대해 일반화시키려 하는 딥 러닝 모델 학습의 특성 때문에 새로운 문제가 대두되기도 하는데, 이후 챕터에서 더 자세히 알아보도록 하자.