[딥러닝 알아듣기] 3.3. 이중 분류기의 구현과 학습 (Binary Classification)

“딥러닝 알아듣기” 시리즈는 딥러닝의 기초 지식을 저만의 방식으로 쉽게 풀어내는 시리즈입니다. 이번 챕터에서는 간단한 이중 분류 모델을 구현해봅니다.

앞서 데이터들의 관계 함수를 찾는 선형 회귀 문제를 딥 러닝 모델로 풀어 보았다. 이번에는 입력 데이터를 두 개의 클래스 로 나누는 이중 분류기(Binary Classifier) 를 학습해보자. 음식의 영양소 함량 데이터를 가지고 그것이 과자인지 아닌지 분류하는 것을 목표로 한다. 먼저 문제 상황과 데이터셋을 이해하고, 주어진 데이터셋으로 이중 분류기를 어떻게 구성하고 학습할 수 있을지 방법을 살펴본다. 이중 분류기의 모델과 데이터셋이 아무리 커지고 복잡해져도, 이번 챕터에서 살펴볼 이론적인 배경에서 크게 벗어나지 않는다. 앞 장에서 PyTorch로 모델을 한 번 구현해 보았으니, 코드상에서 반복되는 부분은 따로 이야기하지 않고 빠르게 넘어가겠다.

3.3.1. 모델 학습 계획 세우기

문제 정의

어떤 음식의 영양소 함량에 따라 그 음식이 과자인지 분류해내고 싶다. 음식에는 수없이 다양한 영양소가 존재하니, 적당히 특징적인 영양소 몇 가지만을 이용해 음식을 과자와 과자가 아닌 것으로 이중 분류 하는 모델을 학습해보자. 영양소 데이터는 탄수화물, 지방, 단백질 등 대표적인 영양소들로만 정리하고, 학습에 필요한 영양소들을 골라서 이중 분류기를 구현하고 성능을 확인하는 과정까지 진행해보자.

입력 특징 엔지니어링

영양소 함량에 따라 과자를 구분해내고 싶다. 그러나 영양소의 종류는 너무도 다양하기 때문에, 어떤 영양소만을 분류에 사용할 것인지 잘 선택해야 한다. 다시 말해서, 입력 데이터의 특징 중 일부만을 적절히 취해야 한다. 음식마다 함량에 큰 차이가 없는 영양소는 분류에 큰 도움을 주지 못할 것이다. 과자 분류의 사례를 보자. 많은 영양소들이 존재하지만, 다른 음식들과 과자를 가장 확실하게 구분해줄 수 있는 영양소는 탄수화물 과 단백질 이다. 어떤 음식의 탄수화물 함량이 상대적으로 높고 단백질 함량이 낮을수록 과자로 구분될 확률이 높다.

방금 우리의 경험을 기반으로 입력 데이터를 엔지니어링했다. 입력 데이터에서 중요한 특징만을 취하고 나머지는 포기하는 결정을 내렸다. 실제로 탄수화물과 단백질 함량에 따라 과자와 과자가 아닌 것이 어떻게 나뉘어 있는지 그래프 상에서 확인해 보자. 과자가 아닌 음식들은 대부분 육류 음식들이다.

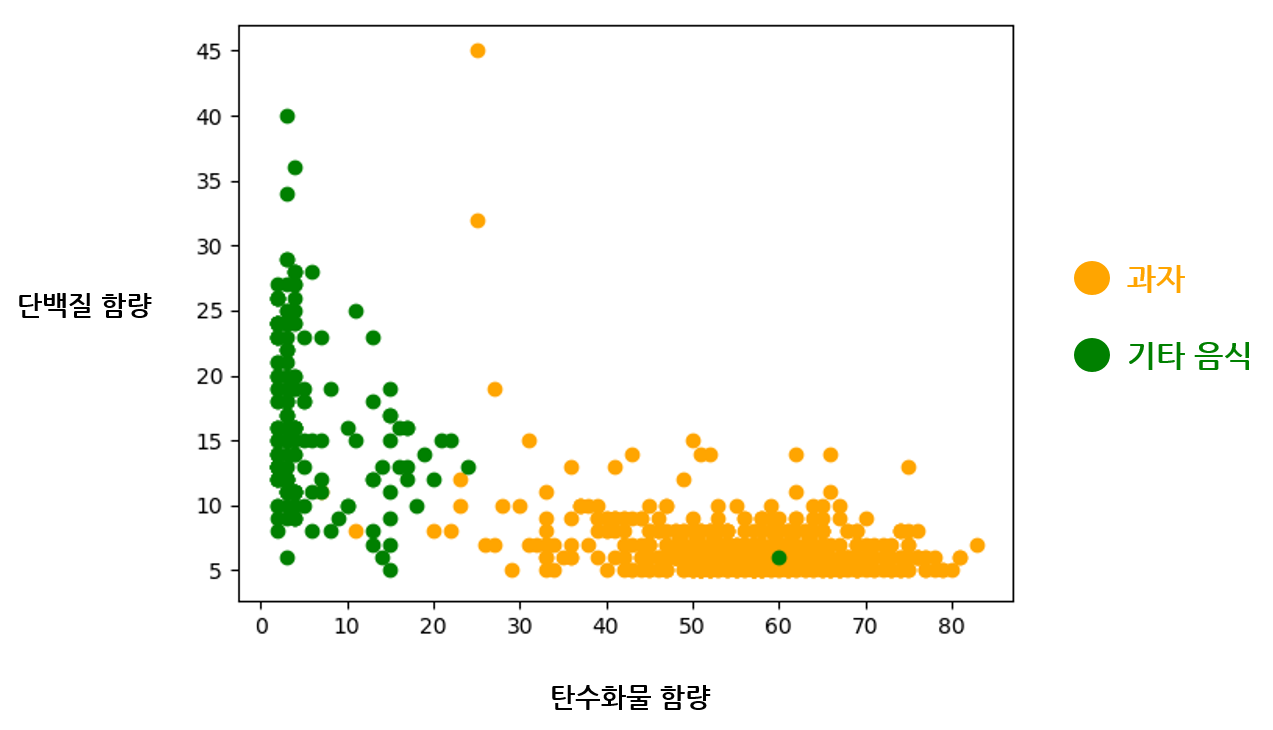
탄수화물과 단백질 함량을 각각 하나의 축으로 하는 그래프에 음식들의 위치를 나타냈다. 하나의 음식은 하나의 점으로 표현되며, 주황색 점이 과자 클래스의 데이터이다. 얼핏 봐도 과자가 확실히 구분되는 것으로 보인다. 단백질과 탄수화물이 아닌 지방 등의 다른 영양소를 사용해 나타냈다면, 위 그림보다 확실하게 과자를 구분하지 못했을 것이다. 이와 같이 모델의 효율적인 학습을 위해 데이터에서 특징을 선택하고 포기하는 과정을 통틀어 특징 엔지니어링(Feature Engineering) 이라고 한다. 넓은 의미에서 보면 데이터 엔지니어링(Data Engineering) 과 비슷한 단어이다.

문제를 풀기 위해 수집한 데이터셋(Raw data)을 그대로 사용하면 모델을 효율적으로 학습할 수 없다. 영양소 데이터를 수집한다고 생각해보자. 정말 수많은 영양소의 종류가 있으며, 데이터를 수집할 때 원하는 영양소만 선택해서 수집하기는 힘들다. 데이터를 수집하는 입장에서는 최대한 다양한 데이터가 있으면 좋으니, 어떤 하나의 값도 버리지 않고 최대한으로 다양한 데이터들을 수집한다. 수집한 데이터를 어떻게 활용할 지 모르기 때문이다.

이렇게 수집된 데이터는 매우 다양한 특징(Feature) 들을 가지고 있다. 어떤 데이터를 표현하기 위한 수치들을 각각의 특징으로 볼 수 있다. 음식 영양소 데이터라면 탄수화물, 단백질, 지방 등 각각의 영양소 함량이 어떤 음식 하나를 표현하기 위한 특징량이 된다. 그리고 각각의 특징을 얼마나 많이 가지고 있는지에 따라 데이터의 종류가 구분된다. 단백질과 탄수화물 함량이라는 특징량의 차이로 과자와 육류가 구분되는 것처럼 말이다.

보통의 경우, 딥 러닝 모델은 입력 데이터에 각각의 특징이 얼마나 많이 포함되어있는지를 보고 출력을 결정한다. 모델의 판단에 상대적으로 큰 도움을 주는 특징과 그렇지 못한 특징이 있을 수 있다. 예를 들어, 과자와 과자가 아닌 음식을 구분하는 일에는 지방 함량이라는 특징보다 단백질 함량이라는 특징이 훨씬 큰 도움을 준다. 둘 중 하나의 특징만을 선택해 모델을 학습해야 한다면 당연히 단백질 함량만을 학습 데이터에 포함시켜야 한다.

사실 데이터의 특징은 다양할수록 좋다. 이상적으로 음식의 수많은 영양소 특징을 동시에 이해해서 음식들을 구분할 수 있다면 금상첨화일 것이다. 그러나 컴퓨터는 생각보다 훨씬 멍청해서, 너무 많은 특징들을 동시에 이해시키려고 하면 헷갈려하기 시작한다. 탄수화물과 단백질 함량만 두고 과자를 구분하면 쉽게 구분해낼 수 있지만, 수많은 식품첨가물의 함량을 모두 던져준 다음 구분해내라고 하면 쉽사리 결정하기 어려울 것이다. 식품첨가물들을 비슷하게 함유한 다른 음식들도 널렸기 때문이다. 하물며 사람도 헷갈릴텐데, 단순히 주어진 데이터로부터 학습만 하는 딥 러닝 모델이 모든 특징의 중요도를 동시에 평가하기는 쉽지 않은 일이다.

그래서 모델에 입력할 특징 자체를 잘 선택해야한다. 최대한 많은 특징 데이터를 살려서 모델에 입력하면 좋겠지만, 모델이 이해할 수 있는 범위 이상으로 다양한 특징 데이터를 던져주면 모델이 헷갈려할 것이기 때문이다. 모델이 학습에 실패할 것이 뻔하니, 현재 풀고 있는 문제에서 중요하다고 생각되는 특징을 신중히 선택해주어야 한다. 중요하지 않은 특징 데이터 수십 개를 포함해서 모델을 학습하는 것보다, 중요한 특징 데이터 몇 개만을 확실하게 이해시키는 것이 모델 성능을 높일 수 있는 중요한 열쇠다. 그래서 특징 엔지니어링은 딥 러닝 모델의 학습에 있어 가장 중요한 과정이다.

다른 문제에도 당연히 데이터 엔지니어링은 중요하지만, 데이터 분류 모델을 학습할 때에는 더욱 신경을 써주어야 한다. 어떤 특징을 취하고 버리는지에 따라 모델의 학습 난이도가 크게 달라지기 때문이다. 이 장에서는 구현의 편의를 위해서 필자가 미리 정제해놓은 데이터를 활용하도록 하자.

앞에서 했던 이야기에 약간 이상한 점이 있다. 최대한 많은 특징 데이터를 사용할수록 좋은데, 모델에 많은 특징 데이터를 입력하면 헷갈려한다니, 모순처럼 느껴진다. 앞으로 딥 러닝 모델의 크기를 키우고 다양한 학습 방법을 공부하면서, 어떻게 많은 특징 데이터를 동시에 사용할 수 있을지 알아볼 것이다.

모델 정의하기

최종적으로 결정된 입력 특징은 음식의 단백질 함량과 탄수화물 함량 두 가지이다. 모델은 두개의 특징량을 입력 데이터로 받고 하나의 값을 출력하도록 만든다. 그 값에 따라 과자를 구분하도록 만들면 될 듯 하다. 모델의 출력을 0에서 1 사이의 실수로 설정하고, 출력이 0에 가까우면 과자, 1에 가까우면 과자가 아닌 음식 으로 판단한 것으로 보자. 일정한 임계값(Threshold) 을 두고 그것을 넘는지 여부를 통해 판단을 결정한다.

이 구조, 어딘가 익숙하다. 우리는 앞서 퍼셉트론 구조를 같이 알아보면서, 이중 분류를 하나의 결정 경계(Decision Boundary) 를 찾는 문제로 정의했었다. 과자를 분류하는 이중 분류 모델도 그와 똑같이 과자와 기타 음식 데이터를 가장 확실하게 구분할 수 있는 하나의 결정 경계를 찾는 문제로 이해할 수 있다. 아마 임계값에 따라 다음 그림과 같은 결정 경계를 찾을 수 있을 것이고, 저 직선을 기준으로 과자를 구분할 것이다.

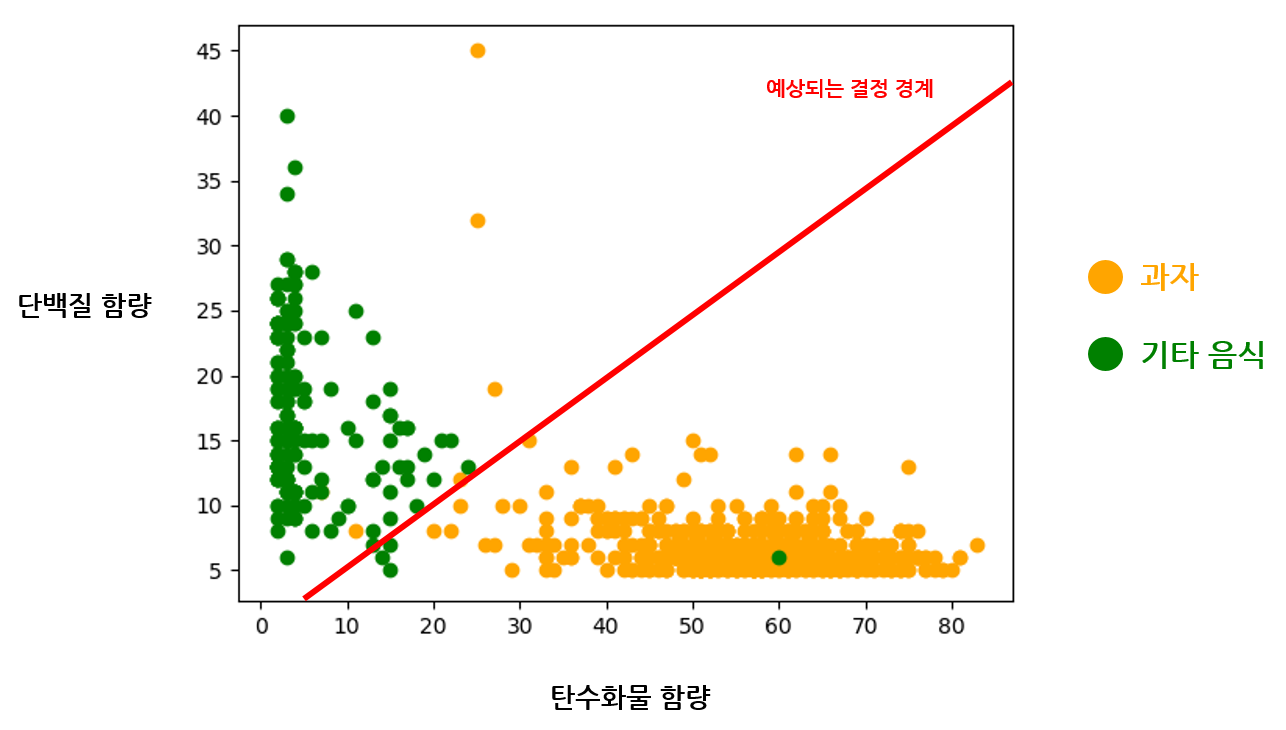
데이터를 구분하려면 먼저 결정 경계를 만들 선형 함수를 하나 찾아야 하고, 그것이 우리가 최적화해야 할 모델이 된다. 입력 데이터는 두 개의 특징을 가지므로 (2 x 1) 텐서이고, 출력 데이터는 (1 x 1) 텐서로 구성하면 된다.

PyTorch로 모델을 아래와 같이 구현할 수 있다. 두 개의 입력 특징 값을 받아 하나의 값을 출력하는 선형 함수를 구현한 모델이다.

nn.Linear(2, 1)

그런데 이중 분류 모델을 학습할 때는 선형 함수의 출력을 그대로 사용하면 안 된다. 모델의 출력이 0에서 1 사이의 실수 값으로 나와야 원래 우리가 생각했던 방법으로 이중 분류를 구현할 수 있기 때문이다. 선형 함수의 출력을 그대로 사용하면 출력의 범위(Boundary)가 고정되지 않는다. 출력의 범위를 0에서 1 사이로 강제하기 위해서는 모델의 활성 함수를 그에 맞게 적용해주어야 한다. 그래서 이중 분류 모델의 활성 함수로 시그모이드(Sigmoid) 함수가 널리 사용된다.

시그모이드 함수는 앞에서 잠깐 본 바가 있다. 입력 값이 작아질수록 출력이 0에 가까워지고, 입력 값이 커질수록 출력이 1에 가까워지는 특성이 있다. 그러나 출력 값이 0과 1 사이를 벗어나지 않아 확실한 출력의 범위가 존재한다. 선형 모델의 출력을 시그모이드 함수에 입력해서 0과 1 사이의 실수 출력 값을 얻어낼 수 있다.

이중 분류 모델의 활성 함수로 시그모이드를 사용해야 하는 이유가 무엇일까? 사실 0에서 1 사이의 출력을 내는 활성 함수는 얼마든지 다양하게 만들 수 있다. 그러나 시그모이드를 사용하는 이유는 그 출력의 형태에 있다. 그래프에도 보이듯이 시그모이드는 입력이 0인 지점을 기점으로 출력이 큰 폭으로 벌어진다. 선형 모델의 출력을 시그모이드에 입력했을 때, 대부분의 경우 0 또는 1의 극한값에 가까운 출력을 보인다. 그만큼 모델이 두 클래스를 0 또는 1로 확실하게 구분해줄 수 있을 것이다. 그래서 시그모이드 활성 함수를 사용한다.

nn.Linear 레이어의 출력을 그대로 시그모이드 함수에 입력해서, 0과 1 사이의 실수 값 출력을 얻어내는 모델로 확장해보자. PyTorch로 여러 단계를 순서대로 거치는 모델을 구현할 때 nn.Sequencial 을 이용할 수 있다. nn.Sequencial 객체 안에 순서대로 거칠 모델의 구조를 정의하면, 정의된 구조에 따라 순차적으로 데이터가 흐르면서 출력을 생성한다. 다음과 같이 모델을 정의해 놓으면, 모델에 데이터가 입력되었을 때 선형 함수를 거친 후 시그모이드 활성 함수를 적용한 출력 데이터가 나온다.

model = nn.Sequencial(
    nn.Linear(2, 1),	# 선형 함수
    nn.Sigmoid()		# 시그모이드 활성 함수
)

이중 분류 모델의 손실 함수

딥 러닝 모델의 올바른 학습을 위해서는 문제와 모델에 맞는 손실 함수를 사용해야 한다. 이중 분류 모델을 학습하고 있으므로, 모델의 출력이 데이터를 틀리게 분류하고 있음을 확실히 보여주는 손실 함수를 정의해야 한다. 모델의 출력과 정답 데이터의 차이가 클수록 손실이 커져야 한다는 기본적인 아이디어는 같지만, 이중 분류 문제의 특성에 맞게 오차를 계산하는 방법을 바꿔주어야 한다.

이중 분류 모델이 잘 학습되었다는 것은, 두 분류의 입력 데이터에 대한 출력의 평균적인 차이가 큰 신경망 모델을 만들었다는 뜻으로 이해할 수 있다. 따라서 이중 분류 모델 최적화의 기준이 되는 손실 함수는, 모델의 출력이 정답에 가까운 방향으로 얼마나 0 또는 1의 극한값에 가깝게 나오는지 정량적으로 확인할 수 있어야 한다.

물론 선형 회귀 문제에서 사용했던 MSE를 손실로 사용해도 학습은 가능하다. 모델의 출력과 정답 데이터의 차이를 손실로 쓰는 것이기 때문이다. 그러나 분류 문제에 있어 더욱 확실한 손실 함수를 정의할 수 있다면, 그것을 사용하는 편이 훨씬 나을 것이다. MSE는 어디까지나 단순히 출력과 정답의 오차를 보기 위해 사용된다. 단순히 값의 차이가 큰지 보는것과 분류를 잘 했는지 보는것은 다른 문제이다. 분류 문제에 적용할 손실 함수는, 값의 차이가 커지면 커질수록 더욱 확실하게 큰 손실을 만들 수 있어야 한다. 모델이 틀리게 분류했음을 더 확실하게 알려주기 위해서이다.

다행히 같은 아이디어에서 출발한 손실 함수가 이미 개발되어 있다. 교차 엔트로피 손실(Cross-Entropy Loss) 이라고 한다. 임의의 입력 데이터에 따른 모델의 출력이 \(\hat{y}\), 정답 데이터가 \(y\)일 때 다음의 수식으로 정의된다.

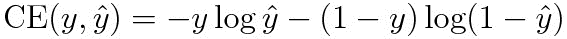
언뜻 보면 식이 복잡해 보인다. 그러나 핵심 아이디어만 확실하게 기억하고 있으면 이해하기 어렵지 않다. 모델의 출력이 정답 데이터에 최대한 가까워야 하고, 정답에서 멀어질수록 손실의 증가 폭이 확실하게 커져야 한다. 이 관점에서 보면, 위의 식을 각각 정답이 0일 때와 1일 때의 오차를 의미하는 두 개의 식으로 나눌 수 있다.

먼저 식의 앞쪽 항부터 살펴보자. \(-y \log \hat{y}\)은 \(y = 0\)일 때 무조건 0이 된다. 정답 데이터 \(y = 1\)일때만 손실에 영향을 주는 항이라는 이야기다. 정답 데이터 \(y = 1\)일 때의 손실을 \(-\log \hat{y}\)로 계산한다고 보면 된다. 모델의 출력에 따른 손실의 변화를 보기 위해서, 함수 \(y = - \log x\)의 그래프를 그려보자.

<그림 4> 함수 의 그래프

\(y = - \log x\)의 그래프에서 확실한 특징 두 가지를 찾아낼 수 있다. \(x\)가 0에 가까워질수록 \(y\)는 양의 무한대로 발산하고, \(x\)가 커질수록 \(y\) 는 음의 무한대로 발산한다. 또한 \(x = 1\) 인 지점에서 \(y = 0\)이다.

다시 손실 함수의 수식으로 돌아와서, \(\hat{y}\)이 0에 가까워질수록 \(- \log \hat{y}\)의 값 또한 양의 무한대로 발산할 것이다. 반대로 \(\hat{y}\)이 1에 가까워지면 \(- \log \hat{y}\)는 0에 가까워진다. 우리가 지금 보고 있는 항이 정답 \(y = 1\)인 경우에 대한 수식이므로, 모델의 출력 \(\hat{y}\)가 1에 가까워질수록 손실이 작아지고 멀어질수록 손실이 기하급수적으로 커져야 한다는 아이디어에 딱 알맞는 수식임을 이해할 수 있다.

뒷 항인 \(-(1-y) \log (1-\hat{y})\)도 같은 원리이다. 이 항은 \(y = 1\)일 때 값이 무조건 0이므로, \(y = 0\)인 경우에만 손실에 영향을 미치는 항이다. \(y = 0\)인 경우 모델의 손실이 \(- \log (1 - \hat{y})\)로 계산된다. 앞과 동일하게 함수 \(y = -\log(1-x)\)의 모양도 확인해보자.

<그림 5> 함수 의 그래프

\(y = 0\)인 경우의 손실로 앞의 그래프와 같은 식을 사용하면, 모델의 출력 \(\hat{y}\)이 0일 때 손실이 0에 가까워지고, 0에서 멀어질수록 손실이 양의 무한대로 발산하게 된다. 앞 항과 같이 이중 분류 모델을 학습하기에 알맞은 손실 함수인 듯 하다.

다시 교차 엔트로피 손실의 전체 수식을 정리해보자. 모델의 출력이 정답 클래스와 얼마나 가까운지에 따라 0에 수렴하거나 양의 무한대로 발산하는 손실 값을 만든다. 또한 교차 엔트로피 손실 함수는 정답 데이터 \(y\)가 0 또는 1 중 어느 클래스인지에 따라 식의 일부분만 손실로써 계산한다. 모델이 정답 클래스와 차이가 큰 출력을 내놓을수록 각각의 손실이 매우 커지게 만든다. 그래서 이중 분류 모델의 학습에 교차 엔트로피 손실이 널리 사용된다. 다른 함수들에 비해 분류 실패에 대한 손실을 크게 키워주기 때문에 분류 모델의 학습을 더 촉진시킬 수 있다.

이중 분류 모델에 사용되는 교차 엔트로피 손실 함수는 PyTorch에서 아래와 같이 구현한다.

loss_function = nn.BCELoss()	# Binary Cross Entropy

그냥 교차 엔트로피가 아닌 Binary Cross Entropy인 이유는, 말그대로 이중 분류 문제에만 사용할 수 있기 때문이다. 위에서 보았던 교차 엔트로피의 수식은 클래스가 3개 이상인 분류 문제에는 적용할 수 없다. 클래스가 3개 이상인 경우를 다중 분류 문제라고 부른다. 다중 분류 모델도 똑같이 교차 엔트로피를 사용하기는 하지만 적용 방법이 약간 다르다. 다중 분류는 다음 챕터에서 자세히 다루어보도록 하자.

3.3.2. 모델 학습하기

이중 분류 모델의 학습 과정을 PyTorch로 구현해 보자. 다음의 사항들을 순서대로 구현한다.

• 학습을 위한 데이터셋 준비하기
• 데이터를 불러오고 정규화(Normalization) 하기
• 데이터로부터 모델 최적화하기

데이터셋 준비하기

앞선 챕터에서 선형 회귀 모델을 구현할 때는, 매 학습 반복마다 임의의 학습 데이터 배치를 추출하는 과정을 직접 구현했다. 데이터 배치 추출이 구현하기 어렵지는 않지만, 모델을 학습할 때마다 배치 추출 알고리즘을 직접 구현하는 것은 보통 귀찮은 일이 아니다. 다행히 PyTorch는 학습 데이터셋의 일부를 선택해 배치로 만들어주는 Dataset 과 DataLoader 클래스를 가지고 있다. 우리가 할 일은 DataLoader가 어떤 형태로 데이터를 뽑아내면 되는지 정의하는 것 뿐이다.

Dataset 클래스는 PyTorch 모델에게 학습시킬 데이터의 모양과 형태를 미리 정의해놓을 수 있도록 인터페이스를 제공한다. Dataset 클래스를 상속받아 우리의 학습 데이터셋에 맞게 재정의할 수 있다.

DataLoader 는 설정된 Dataset에서 정해진 배치 크기만큼 학습 데이터를 불러오는 역할을 한다. 임의로 학습 데이터를 선택하는 알고리즘이 미리 구현되어 있으므로, Dataset만 잘 정의해서 사용하면 된다. 또한 DataLoader는 데이터의 병렬 로딩을 지원한다. 2대 이상의 GPU를 사용할 때 여러 GPU 디바이스에 입력되는 배치들을 알맞게 병렬로 불러오기 위한 기능이다. PyTorch가 다중 GPU상에서 연산을 어떻게 처리하는지는 향후에 살펴보는 것으로 하고, 이번 챕터에서는 병렬 데이터 로딩은 사용하지 않는다.

먼저 Dataset을 상속받아 음식 영양소 정보와 정답 클래스를 동시에 가지고 있는 Food Dataset 을 구현해보자. Dataset 내에는 다음의 두 메소드가 필수로 오버라이딩 되어있어야 한다. 후에 DataLoader가 이 메소드들을 사용하여 데이터를 꺼내기 때문이다.

• __len__: Dataset의 전체 길이를 반환한다.
• __getitem__: Dataset의 데이터 하나를 반환한다.

import csv
import random
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader

CLASSES = {
    'meats': 0,		# 클래스 이름이 meats일 경우 정답 클래스는 0
    'snacks': 1		# 클래스 이름이 snacks일 경우 정답 클래스는 1
}

class FoodDataset(Dataset):
    def __init__(self, csv_filename):
        # CSV 파일 내의 전체 데이터셋 로딩
        self.x_datas, self.y_datas = self.data_reader(csv_filename)
        self.data_count = len(self.x_datas)

    # 데이터셋의 총 길이를 반환하는 메소드
    def __len__(self):
        return self.data_count

    # 모델 입력 데이터와 정답 데이터 쌍을 반환하는 메소드
    def __getitem__(self, idx):
        # PyTorch 텐서로 바꾸어 반환
        tensor_x = torch.as_tensor(self.x_datas[idx])
        tensor_y = torch.as_tensor(self.y_datas[idx])
        return tensor_x, tensor_y

    # CSV 파일에서 데이터를 읽어오는 메소드
    def data_reader(self, csv_filename):
        csvfile = open(csv_filename, 'r')
        reader = csv.reader(csvfile)		# CSV 파일 열기	
        x_list, y_list = [], []
        for row in reader:
            class_name = row[0]						# 각 행의 0번째 열은 클래스 이름
            xdata = [float(row[1]), float(row[2])]	# 모델 입력 데이터
            ydata = [CLASSES[class_name]]			# 정답 데이터
            x_list.append(xdata)					# 입력 데이터 리스트에 추가
            y_list.append(ydata)					# 정답 데이터 리스트에 추가
        
        # numpy 배열로 바꾸어 반환
        x_list = np.array(x_list, dtype=np.float32) 
        y_list = np.array(y_list, dtype=np.float32)
        return x_list, y_list

코드에서 중점적으로 봐야 할 부분은 data_reader 메소드와 __getitem__ 메소드이다. 음식 영양소 데이터를 읽어와서 메모리에 적재하고, 학습을 위해 임의의 데이터를 꺼내는 작업까지 모두 클래스 FoodDataset에 정의해놓았다. data_reader 함수가 호출되면 CSV 파일에서 데이터셋 전체를 읽어와서 numpy 배열로 적재한다. 이후에 __getitem__ 함수가 호출되면 적재해놓은 데이터에서 인자로 넘어온 위치(idx)의 입력과 정답 데이터 한 쌍을 PyTorch 텐서로 반환한다. 이후에 DataLoader가 내부적으로 이 함수를 사용해 데이터를 불러올 것이다. DataLoader는 Dataset 추상 클래스에 정의된 인터페이스를 바탕으로 데이터 배치를 로딩하기 때문에, 어떤 데이터셋이라도 정해진 Dataset 인터페이스에 맞게 구현해야 한다.

데이터의 정규화

데이터를 불러오는 클래스와 함수를 모두 다 작성했지만, 그대로 모델 학습에 사용하면 최대의 성능을 끌어내기 힘들다. 이유는 입력 데이터의 각 특징의 수치적인 범위(Scale) 가 다르기 때문 이다. 영양소 데이터의 분포를 다시 보자.

탄수화물 함량은 약 80에 가까운 최댓값을 가지고 있지만, 단백질 함량의 최댓값은 약 40으로 두 배정도 차이가 난다. 이렇게 특징별로 값의 범위가 크게 차이나는 데이터를 그대로 사용하면 모델을 효과적으로 학습할 수 없다. 모델이 모든 특징에 대해 일관적인 학습을 하지 못하고, 값의 범위가 상대적으로 큰 특징만 더 중요하게 판단하도록 학습된다. 모델은 상대적으로 큰 범위의 값을 가지는 특징의 영향을 더 크게 고려하도록 학습될 수 밖에 없다. 똑같이 입력 값에 0.1을 곱하는 선형 함수가 있더라도 10을 입력하는 것과 1,000을 입력하는 것은 출력에 큰 차이를 가져다주는 것처럼 말이다.

그래서 데이터를 학습에 사용하기 전에 먼저 정규화(Normalization) 를 해주어야 한다. 정규화는 입력 데이터에서 모든 특징 값의 범위를 일정하게 맞추기 위한 작업이다. 보통 모든 특징이 0에서 1 사이의 값을 가지도록 만든다. 원본 데이터의 특징 값들은 매우 다양한 범위를 가지고 있지만, 정규화를 거치면 모두 0에서 1 사이의 값으로 맞춰진다. 따라서 모델이 모든 특징을 비슷한 비중으로 이해할 수 있게 된다. 대표적인 정규화 방법으로 다음의 두 가지를 꼽을 수 있다.

• Min-Max Scaler
• Standard Scaler

Min-Max Scaler

널리 쓰이는 정규화 방법 중 하나인 Min-Max Scaler 를 알아보자. 각 특징의 최댓값과 최솟값 사이를 일정한 비율로 나누어 특징 값을 0에서 1 사이로 맞추는 방법이다. 수식으로는 다음과 같이 표현된다.

\(x_\text{min}\)과 \(x_\text{max}\)는 각각 특징의 최솟값과 최댓값을 의미한다. 현재 값을 데이터의 최댓값으로 나누어, 특징 범위 내에서의 상대적인 위치를 특징 값으로 다시 취한다. 방법이 단순해서 구현하기도 쉽다. FoodDataset 클래스에 단백질 함량과 탄수화물 함량 특징 값에 적용할 Min-Max Scaler를 구현해보자.

# 값을 정규화하는 함수
def normalize(self, x, xmin, xmax):
    return (x - xmin) / (xmax - xmin)

# 하나의 특징 열에 대한 정규화 수행
def column_min_max_scale(self, feature_data_list):
    xmin, xmax = min(feature_data_list), max(feature_data_list)
    scaled_list = [self.normalize(x, xmin, xmax) for x in feature_data_list]
    return scaled_list

# 전체 데이터셋에 대한 정규화 수행
def scale_data(self, datas):
    scaled_columns = []
    for i, column_datas in enumerate(datas.T):
        scaled = self.column_min_max_scale(column_datas)
        scaled_columns.append(scaled)
        return np.array(scaled_columns).T

데이터셋에서 하나의 열(Column)은 하나의 특징 값 리스트이므로, 각각의 열마다 최솟값과 최댓값을 구해 정규화를 수행하는 함수를 작성하였다. column_min_max_scale 함수가 하나의 열을 정규화하는 함수이다. scale_data 함수는 전체 데이터셋을 각 열으로 쪼개 정규화하는 함수에 입력하고, 결과를 취합해 정규화된 데이터셋을 돌려준다. FoodDataset이 입력 데이터셋을 불러오는 부분에 scale_data 함수만 한 번 적용해주면 정규화된 입력 데이터셋을 얻어낼 수 있다. 데이터를 읽어오는 함수인 data_reader의 반환 부분을 다음과 같이 수정한다.

def data_reader(self, csv_filename):
    ...
    return scale_data(x_list), y_list			# 입력 데이터셋은 정규화해서 반환

우리 데이터셋에서 단백질 함량 특징을 정규화하면 데이터가 다음과 같이 분포된다.

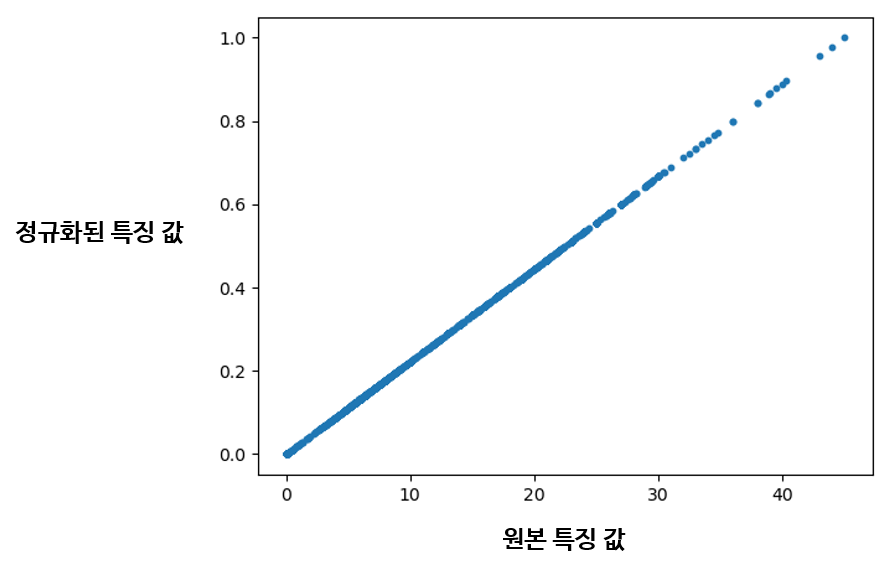
원본 특징 값이 0과 1 사이의 값으로 알맞게 재분포된 결과를 볼 수 있다.

Standard Scaler

또 다른 정규화 방법으로 Standard Scaler 가 있다. Min-Max Scaler는 모든 데이터를 단순히 0과 1 사이의 값으로 변환해주는 작업을 했다. 그런데 정말 모든 특징을 비슷한 범위에서 보고 싶다면, 모든 특징 값의 분포 자체를 비슷하게 만들어주어야 할 필요가 있다. 모든 특징 값의 분포가 평균 0과 표준편차 1의 정규분포를 따르면 좋겠다.

어떠한 분포를 표준정규분포로 변환하는 작업을 표준화(Standardization) 라고 한다. Standard Scaler는 특징 값의 분포를 표준화해서, 모든 특징 값들이 표준정규분포의 범위 내에 일정하게 분포하도록 만든다. Standard Scaler로 정규화하는 방법을 표준화라고 따로 부르기도 한다.

특징 값을 표준화하기 위해 다음의 식을 사용한다. 확률분포를 표준화하는 공식과 동일하다. 식을 이용해 표준화된 값을 Z-Score 라고 부르기도 한다.

\(\mu\)는 특징 값의 평균, \(\sigma\)는 표준편차이다. 현재 값에서 평균을 빼고 표준편차로 나누어서, 평균을 0으로 만들었을 때 특징 값 \(x\)가 평균에서 얼마나 떨어져 있는지 계산한다. 이렇게 계산한 Z-Score 자체를 변환된 특징 값으로 사용하면 표준화가 완료된다. Z-Score로 변환된 특징 값들이 자연스럽게 평균이 0이고 표준편차가 1인 정규분포를 따르기 때문이다. 데이터셋에서 어떤 하나의 열을 표준화하는 함수를 파이썬으로 아래와 같이 구현할 수 있다.

# Z-Score를 구하는 함수
def standardize(x, avg, std):
    return (x - avg) / std

# 하나의 열을 표준화하는 함수
def column_standardize(feature_data_list):
    avg, std = np.mean(feature_data_list), np.std(feature_data_list)
    standardized_list = [standardize(x, avg, std) for x in feature_data_list]
    return standardized_list

앞에서 구현한 column_min_max_scale 함수와 같이 하나의 특징 열을 받아서 표준화한다. numpy.mean 함수와 numpy.std 함수는 각각 리스트의 평균과 표준편차를 구해 준다. 구현한 column_standardize 함수로 단백질 함량 특징 값을 표준화하면 다음과 같은 결과를 얻는다.

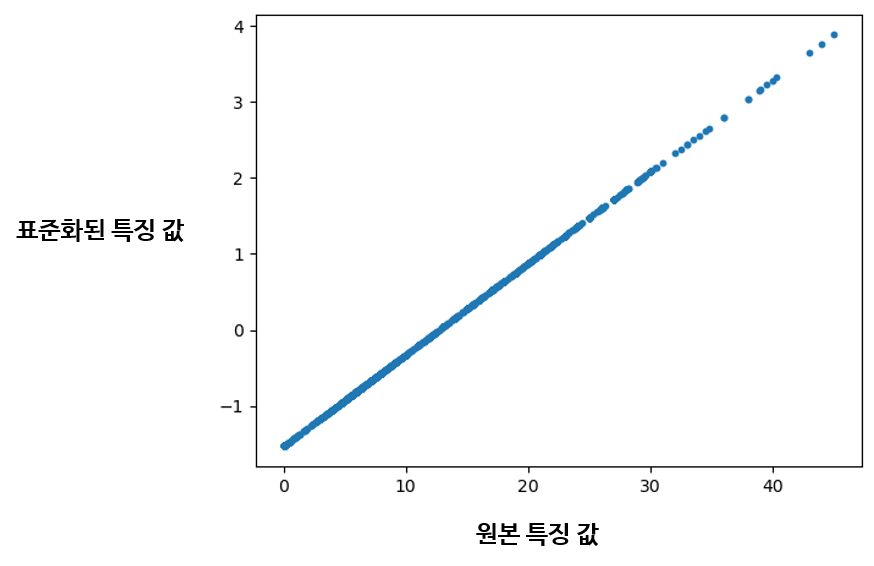
표준화된 결과 값에 주목하자. 평균을 기준으로 Z-Score를 계산했기 때문에 값이 음수로도 분포한다. 또한 Min-Max Scaler를 이용한 정규화처럼 특정 범위로 우겨넣지 않기 때문에, 절댓값 자체가 더 넓게 분포하는 모습을 볼 수 있다.

데이터셋의 정규화와 표준화는 상황에 따라 적절히 적용하면 모델 성능 향상에 큰 도움을 준다. 이번 챕터의 영양소 데이터셋은 분포가 그리 다양하지 않으므로, Min-Max Scaler를 적용한 데이터 정규화만 수행해서 모든 특징 값의 범위를 맞추도록 하겠다.

이상치 제거

앞에서 두 가지 방법을 사용해 특징 값을 정규화해서 학습을 위한 데이터셋 준비는 끝난 것처럼 보인다. 그러나 학습 데이터셋에는 아직 확인하지 않은 큰 위험이 하나 존재한다. 바로 데이터 사이의 __이상치(Outlier)__이다. 이상치는 전체적인 특징 값의 분포와 동떨어진 특징 값을 의미한다.

하나의 예를 들어보자. 현재 우리 데이터셋의 단백질 함량 특징 값은 잘 정규화되어 있는 상태이다. 크게 튀는 이상치가 없었기 때문에, 모든 특징 값이 0과 1 사이에서 적당한 값으로 분포되고 있다.

실제로는 그럴 일이 거의 없겠지만, 만약 단백질 함량이 100이나 되는 이상치 특징 값이 새로 추가된다면 특징 값 분포의 양상은 다음 그림처럼 판이하게 바뀔 것이다.

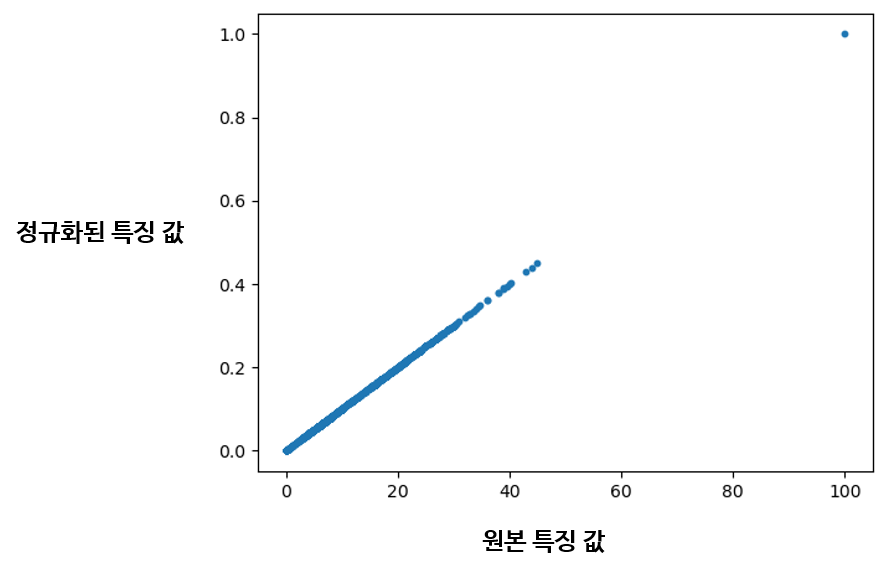
이상치 데이터 단 하나가 추가되었음에도, 0에서 1 사이로 골고루 분포하던 특징 값들이 모조리 0.5 이하로 우겨넣어졌다. 정규화 결과에서도 추가된 이상치 하나만 동떨어져있는 모습을 볼 수 있다. Min-Max Scaler가 단순히 특징의 최댓값과 최솟값 사이 범위로 특징 값을 나누어 정규화하기 때문이다. Standard Scaler를 사용해도 값의 범위만 다를 뿐이지 동일한 현상이 발생한다.

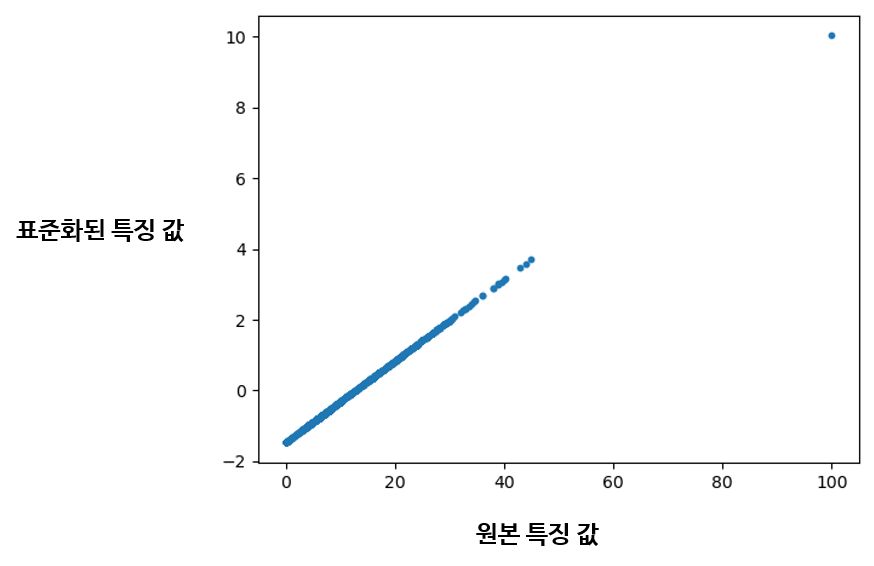
특징 값들이 정규화되어 절댓값이 작아진 상태에서 몇몇 이상치로 인해 대부분의 값이 좁은 구간에 몰리게 되면, 수많은 특징 값들의 차이가 줄어들어 모델 학습이 어려워질 것이다. 원본 특징 값은 절댓값이 매우 커서 이상치로 인한 악영향이 상대적으로 적었다고 해도, 정규화 후에 매우 작은 값으로 몰리기 때문에 문제가 발생한다. 따라서 데이터셋에서 이상치의 영향을 줄일 수 있는 방법이 필요하다.

이상치는 상대적인 갯수가 많지도 않으면서 해당 특징의 전체적인 분포와 동떨어져 있어 골치아프게 만든다. 가장 근본적인 해결 방법은 이상치를 제거 하는 것이다. 단순히 어떤 특징 값이 해당 특징의 평균으로부터 일정 수준 이상 떨어져 있으면 지우는 방안을 택할 수 있다. 보통의 경우 Z-Score 를 특징 값과 평균 사이의 거리로 판단한다. Z-Score가 일정 이상이면 이상치로 판단하고 지우는 방법을 사용할 수 있다.

그러나 Z-Score만을 보고 이상치 데이터를 판단해 지우는 것은 많은 상황에서 위험할 수 있다. 이상치 데이터를 면밀히 분석해보기 전에 무작정 지우면 안 된다. 데이터셋에서 이상치 특징 값들이 정말 아무 의미 없는 데이터인지 확실하게 확인해보아야 한다.

모델과 최적화 과정 구현하기

학습 데이터셋의 준비가 완료되었으니, 이제 학습할 모델과 최적화 기법을 정의하자. 모델은 두 개의 특징 값을 입력받아 하나의 값을 출력한다. 이에 맞춘 선형 함수 하나와 시그모이드 활성 함수를 순서대로 거치도록 하자. 모델의 손실로는 교차 엔트로피(Binary Cross Entropy)를 사용하고, 최적화 기법은 확률적 경사하강법(SGD)을 이용한다. 학습률은 0.01이 적당하다. 모델만 main 블럭에 정의해놓고, 학습의 모든 과정은 train 함수 내에 구현하자.

# nn.Sequential 안에 선언된 순서대로 데이터가 흐른다.
model = nn.Sequential(
    nn.Linear(2, 1),	# 선형 함수
    nn.Sigmoid()		# 시그모이드 활성 함수
)

def train():
	lf = nn.BCELoss()		# 교차 엔트로피 손실 함수
	optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

모델 학습하기

정의한 모델을 최적화하는 코드를 작성하자. 먼저 모델에 입력할 배치의 크기와 최적화 반복 횟수 등 모델 학습에 필요한 파라미터들을 정한다.

batch_size = 256		# 학습 데이터 배치의 크기
max_epochs = 10000		# 에폭의 수

배치의 크기를 256으로 설정했으므로, 최적화 과정에서 모델에는 한 번에 256쌍의 학습 데이터가 사용된다. 또한 학습해야 할 에폭의 수를 10,000번으로 설정했다. 전체 데이터셋을 10,000번 반복해 학습해야만 학습이 종료된다.

다음으로, 배치 사이즈에 맞추어 Dataset에서 데이터를 꺼내오는 DataLoader를 아래와 같이 선언할 수 있다.

dataset = FoodDataset('./openfoodfacts_binary_train.csv')
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

앞서 정의한 FoodDataset 내의 데이터를 배치 크기에 맞춰 무작위로 뽑아내주는 DataLoader를 선언했다. shuffle=true 옵션을 주면 무작위 순서로 데이터를 선별해서 배치를 만들어준다. false일 경우에는 학습 데이터 리스트의 순서대로 배치를 만들어준다.

이제 선언한 dataloader를 통해 학습 반복을 수행해보자. DataLoader 객체는 Iterable 하다. 따라서 for 반복으로 dataloader를 순회하면서 학습 데이터 배치를 가져올 수 있다. DataLoader는 자신에게 할당된 Dataset의 __getitem__ 메소드를 정해진 배치 크기만큼 호출해서 데이터 배치를 만들어낸다.

loss_sum = 0

for epoch in range(max_epochs):
    for batch_num, samples in enumerate(dataloader):
        x_data, y_data = samples		# 학습 데이터 쌍을 불러온다.
        predict = model(x_data)			# 모델의 출력을 얻어낸다.
        loss = lf(predict, y_data)		# 출력과 정답 사이의 교차 엔트로피 손실을 계산한다.
        loss_sum += loss.item()

       	# 계산한 손실로 최적화를 한 스텝 진행한다.
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    # 매 에폭마다 평균 손실 확인
    avg_loss = loss_sum / batch_num
    print('Epoch : {}, Current loss : {}'.format(epoch, avg_loss))
    loss_sum = 0.0

코드를 실행해보면 반복한 에폭 수가 늘어남에 따라 손실이 잘 줄어드는 것을 확인할 수 있다.

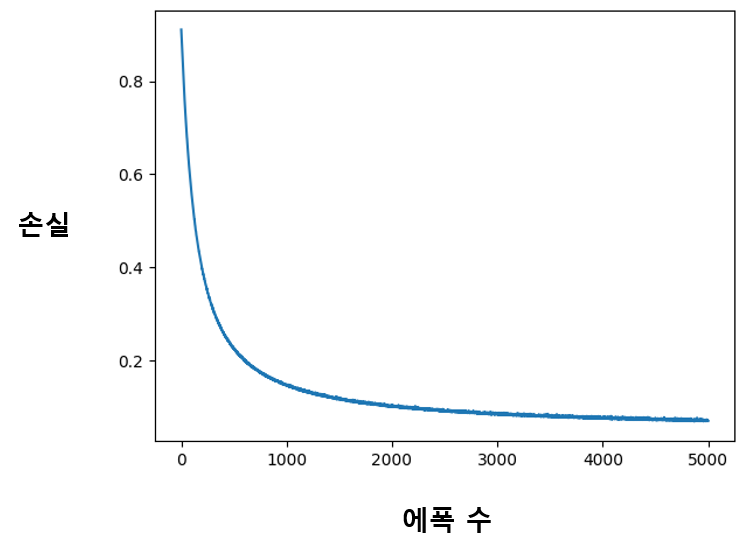
학습한 모델로 추론 실행하기

모델을 학습만 하면 의미가 없다. 실제로 모델에 데이터를 입력해서 0 또는 1 클래스로 분류한 결과를 확인할 수 있어야 한다. 현재 우리 모델의 출력은 시그모이드 활성 함수를 거친 직후의 값이므로 연속적인 실수 형태이다. 모델의 출력 값에 따라 모델이 둘 중 어느 클래스로 분류하고 있는지 확실하게 만들어줄 임계값(Threshold) 이 필요하다. 시그모이드 활성 함수로 인해 모델이 0 또는 1에 수렴하는 출력을 내놓도록 학습했으므로, 중간값인 0.5 를 임계값으로 두어 모델이 분류한 클래스를 구분하도록 하자.

모델의 출력을 통해 0 또는 1의 클래스로 이중 분류해주는 함수를 간단히 구현할 수 있다.

def inference(model, data):
    threshold = 0.5
    preds = model(data)
    binarized_preds = []
    for p in preds:
        p = (p > threshold)   # 모델의 출력이 threshold 이상일경우 True, 그렇지 않으면 False
        p = p.int()     # True: 1, False: 0으로 변환
        binarized_preds.append([p.item()])
    preds = torch.as_tensor(binarized_preds)
    return preds

실제로 모델을 이용해 우리가 원했던 형태의 출력을 얻는 과정을 추론(Inference) 라고 한다. 우리 모델을 실제로 추론에 이용하려면 inference 함수를 거쳐 출력이 0 또는 1 둘중 하나로 나오도록 해야 한다. 당장 모델의 성능을 평가할때도 모델을 이용해 추론 결과를 얻는 과정이 필요하다.

사실 임계값의 설정 또한 모델의 성능에 매우 중요한 영향을 끼치므로, 무조건 0.5로 설정하는 것은 바람직하지 않다. 임계값이 바뀌면 모델의 추론 결과도 달라지기 때문이다. 모델의 성능을 최대한으로 끌어낼 수 있는 임계값의 설정 방법은 모델의 평가 방법과 연결된다. 학습 결과를 평가해보면서, 적절한 임계값을 설정하는 방법 또한 같이 알아보도록 하자.

3.3.3. 학습 결과 평가하기

정해진 반복만큼 최적화를 완료하면, 우리 모델의 성능을 평가해보아야 한다. 미리 준비한 평가 데이터셋으로 학습 결과를 평가해보자.

분류 정확도로 평가하기

이중 분류 모델의 성능 평가를 위한 평가 지표를 선정해 보자. 앞서 말했다시피 평가 지표를 어떻게 정의하는지에 따라 모델의 성능 측정 결과가 크게 달라질 수 있다. 직관적으로 가장 먼저 떠오르는 평가 지표는 단순 분류 정확도(Accuracy) 이다. 단순히 모델이 추론한 클래스가 정답 클래스와 동일한지 여부만 보는 평가 지표다. 정확도의 계산은 간단하게 구현할 수 있다. 전체 평가 데이터 갯수 중 모델이 정확하게 분류한 데이터 갯수의 비율을 구하면 된다.

정확도 = 분류 성공 개수 / 전체 데이터 개수

모델의 출력과 정답 데이터를 이용해 정확도를 계산하는 함수를 구현해 보자. 추론 결과 데이터 배치와 정답 데이터 배치의 갯수만 맞으면 사용할 수 있으며, 우리는 평가 데이터셋 전체를 넣어서 정확도를 계산할 것이다.

def calc_accuracy(inf_result, y_data):
    correct_count = 0
    bsize = len(inf_result)		# 전체 데이터 갯수
    for i in range(bsize):
        if inf_result[i] == y_data[i]:
            correct_count += 1			# 모델의 추론이 정답을 맞춘 갯수를 센다.
    avg_accuracy = float(correct_count) / float(bsize)	# 정확도를 계산한다.
    return avg_accuracy

모델의 평가 지표를 정의했으니, 평가 데이터셋 전체에 대한 모델의 정확도를 구하는 함수 test를 정의해서 모델을 평가해보자. 평가 데이터셋 또한 학습 데이터셋과 구조가 동일하므로, 같은 FoodDataset을 이용하여 데이터를 불러오겠다.

def test(model):
    dataset = FoodDataset('./openfoodfacts_binary_test.csv')
    dataloader = DataLoader(dataset, batch_size=len(dataset))	# 배치 크기 = 데이터셋 전체
    x_data, y_data = next(iter(dataloader))		# 평가 데이터셋 전체 로딩
    preds = inference(model, x_data)			# 모델 추론 결과 생성
    accuracy = calc_accuracy(preds, y_data)		# 전체 데이터셋에 대한 정확도 계산
    print('Accuracy: {}'.format(accuracy))

dataloader를 선언할 때, 배치의 크기로 FoodDataset의 전체 데이터셋 크기를 넣어 주었다. 배치를 한 번 불러오면 전체 데이터셋이 나온다는 이야기다. 그러므로 x_data, y_data에는 평가 데이터셋 쌍 전체가 들어 있다. 이를 이용해 평가 데이터셋 전체의 추론 결과를 구하고 정확도를 계산한다.

아마 앞의 과정을 잘 따라왔다면 평가 데이터셋에서의 높은 정확도를 볼 수 있을것이다.

Accuracy: 0.9811320754716981

모델의 분류 결과가 평가 데이터셋의 98.11%에 대해 정답이었다. 이중 분류 모델이 어느 정도 잘 학습되었음을 확인할 수 있었다.