“딥러닝 알아듣기” 시리즈는 딥러닝의 기초 지식을 저만의 방식으로 쉽게 풀어내는 시리즈입니다. 이번 챕터에서는 다중 분류기 신경망을 구현해보고, 신경망의 구현 과정에서 일어나는 역전파 과정에 대해서 알아봅니다.
이번에는 분류할 클래스의 개수를 늘려 보자. 세 개 이상의 클래스로 데이터를 분류하는 문제를 다중 분류(Multi-Class Classification) 문제라고 한다. 여러 개의 클래스로 입력 데이터를 구분하는 다중 분류 모델을 학습하면서, 여러 층으로 쌓인 딥 러닝 모델을 어떻게 학습시키는지 알아보도록 하자. 이번 챕터까지의 내용은 앞으로 딥 러닝의 어떤 세부 분야를 공부하더라도 필수적으로 이해해야 할 기본 지식들이다.
3.4.1. 모델 학습 계획 세우기
문제 정의
영양소 데이터에 따른 음식 분류를 확장하고자 한다. 앞 챕터에서 이중 분류 모델을 구현해볼 때, 영양소 데이터에 따라 음식을 과자와 과자가 아닌 음식으로 구분하는 모델을 만들었다. 이 문제를 확장해서, 더 다양한 종류의 영양소 데이터를 입력받아 더 많은 클래스로 음식을 구분하는 모델을 만들어보자. 분류할 음식의 종류를 과자, 육류, 음료수, 디저트 의 4가지로 늘릴 것이다. 분류할 클래스가 늘어나면 당연히 입력 데이터도 더 많은 정보를 담고 있어야 하고, 모델도 더욱 복잡해져야 할 것이다.
입력 데이터 엔지니어링
분류해야 할 음식의 종류가 많아지면 탄수화물과 단백질 함량 두 가지의 데이터만으로 음식을 구분하기 어려워진다. 음식 데이터의 분포를 그래프에 그려보면 확실히 네 개의 클래스를 분류하기 힘들어보인다.
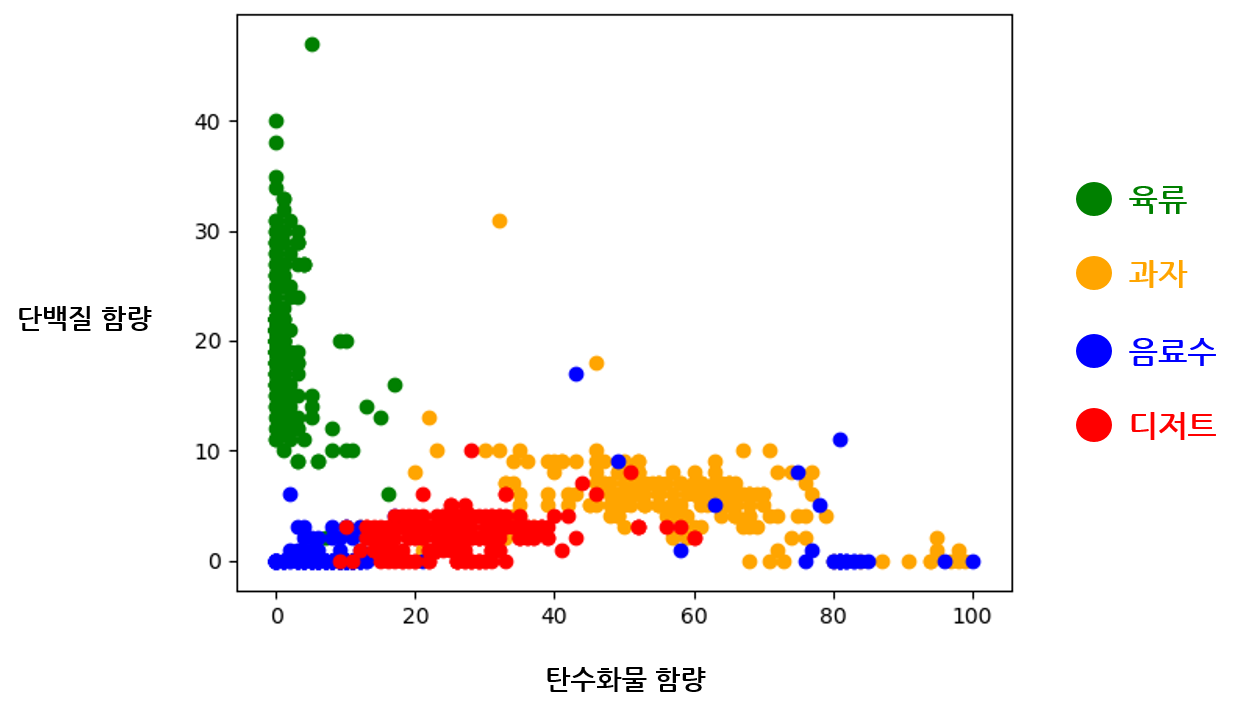
특히 음료수와 디저트의 경계가 모호하다. 이 데이터를 가지고 음료수와 디저트만을 이중 분류하는 모델을 학습하려고 하면 분명 학습이 힘들 것으로 보인다. 두 영양소의 함량이 동일하게 겹쳐 있는 데이터가 많아 하나의 결정 경계를 찾기가 어렵기 때문이다. 음료수와 디저트를 구분해내려면 입력 데이터에 단백질과 탄수화물 함량 말고도 추가적인 정보가 필요하다. 다시 말해, 입력 데이터의 특징 종류 가 늘어나야 한다. 분류해야 할 클래스가 많아졌으니 입력 데이터도 더욱 다양한 정보를 담고 있어야 하기 때문이다. 다중 분류 모델의 학습을 위해 입력 데이터의 특징 갯수를 다음과 같이 네 가지로 늘려서 활용해보도록 하자. 미리 준비된 데이터셋 파일을 사용하면 된다.
- 단백질 함량
- 탄수화물 함량
- 지방 함량
- 식품첨가물 함량
식품 첨가물 함량의 경우 엄밀히 말하면 영양소는 아니지만, 음식 분류에 큰 도움을 줄 가능성이 있는 특징이므로 데이터에 같이 포함하였다.
다중 분류 모델의 손실 함수
입력 데이터의 특징 갯수가 네 가지이고 출력 클래스의 갯수가 네 가지인 다중 분류 모델을 정의해야 한다. 다중 분류 모델은 이중 분류 모델의 아이디어를 확장해서 만들 수 있다.
이중 분류 모델은 최대한 많은 데이터를 각각의 클래스로 정확히 구분해낼 수 있는 하나의 결정 경계를 찾기 위해 학습했다. 그러나 다중 분류 모델은 동시에 여러 개의 클래스로 데이터를 구분해야 하기 때문에, 하나의 결정 경계만으로 모든 클래스를 분류해낼 수 없다. 그래서 다중 분류 문제는 기본적으로 여러 개의 이중 분류기를 동시에 사용하는 방식으로 접근한다. 아래의 네 가지 상황에 맞는 이중 분류 모델을 동시에 학습해서 사용한다면, 각 모델의 결과를 모두 합쳐 데이터를 하나의 클래스로 특정할 수 있을 것이다.
- 입력 데이터의 음식이 육류 인지 아닌지 분류
- 입력 데이터의 음식이 과자 인지 아닌지 분류
- 입력 데이터의 음식이 음료수 인지 아닌지 분류
- 입력 데이터의 음식이 디저트 인지 아닌지 분류
당연한 이야기지만 네 개의 서로 다른 모델을 동시에 학습시키는것은 비효율적인 일이다. 하나의 모델 출력만으로 위의 네 가지 상황을 모두 확인해볼 수 있는 방법이 필요하다. 직관적으로 생각해보았을 때, 모델의 출력 벡터 길이를 클래스 개수와 맞추면 좋을 듯 하다. 길이가 4인 벡터가 될 것이다. 출력 벡터의 각 요소를 모델이 해당 클래스로 판단하는데에 가지는 확신의 정도로 해석하면 좋겠다. 예를 들면 다음과 같이 말이다.
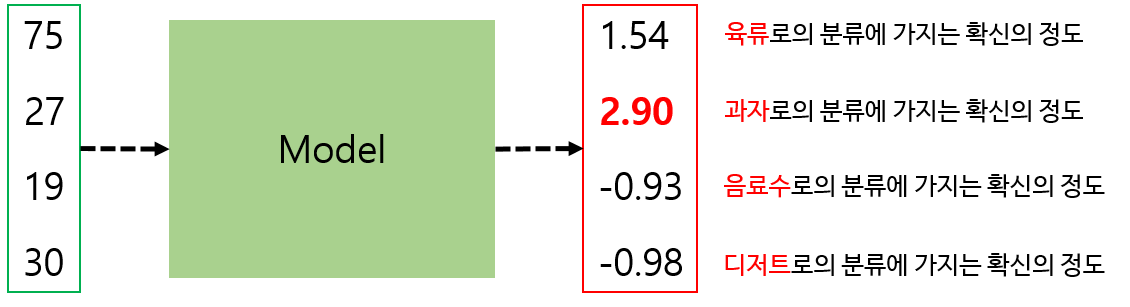
출력 벡터의 각 요소를 모델이 해당 클래스로의 분류에 가지는 신뢰도(Confidence) 로 해석할 수 있다. 신뢰도가 가장 높은 클래스를 모델이 분류한 클래스로 본다. 이 방법으로 접근하면 하나의 모델만으로 다중 분류를 학습할 수 있을 것이다.
그러나 모델의 출력 값을 그대로 각 클래스에 대한 신뢰도로 사용하지는 않는다. 확실한 신뢰도의 계산을 위해 소프트맥스(Softmax) 라는 이름의 활성 함수를 모델의 출력에 적용할 것이다. 소프트맥스 활성 함수를 수식으로 보면 다음과 같다.
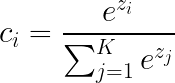
식이 의미하는 바는 간단하다. 모델이 계산한 출력 벡터의 총합에 대해 각각의 요소들이 가지는 비율 을 계산한다. 다만 이 비율을 계산할 때 출력 벡터의 모든 요소에 밑이 e인 지수함수를 적용한다. 이렇게 하면 출력 벡터 내의 값이 작을 때와 클 때의 비율 차이가 크게 벌어지는 결과를 가져온다. 가장 출력 값이 높은 클래스에 다른 클래스보다 훨씬 큰 신뢰도를 부여하는 것이다.
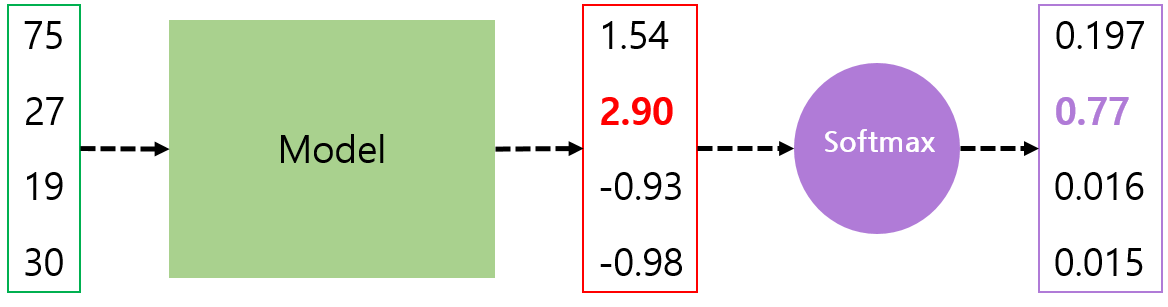
소프트맥스 함수를 거치면 출력 벡터의 총합이 1이 된다. 원래 출력 벡터의 총합에 대한 각 요소들의 비율이라서 그렇다. 또한 소프트맥스 함수를 거친 출력 벡터를 보면, 작은 값과 큰 값 사이의 차이가 더욱 크게 벌어진 것이 보인다. 비율에 지수 함수를 적용했기 때문이다. 모델의 출력이 각각 1.54와 2.90으로 약 두배 정도밖에 차이가 나지 않지만, 소프트맥스 함수를 거치면 0.197과 0.77로 차이가 크게 벌어지게 된다. 이렇게 소프트맥스 함수는 신뢰도가 가장 높은 클래스와 그렇지 않은 클래스들 간의 차이를 크게 만들어주는 역할을 한다. 이렇게 하나의 클래스만을 강하게 신뢰하도록 만들면, 클래스 예측에 실패했을 시에 그 정보를 모델에게 더욱 강하게 전달할 수 있을 것이다. 현재 모델이 가지는 더욱 확실한 손실 값을 계산할 수 있다는 이야기이다. 소프트맥스 함수를 사용하지 않아도 다중 분류기의 학습은 가능하지만, 소프트맥스를 사용했을 때보다 좋은 성능을 기대할수는 없다.
소프트맥스 함수를 사용해야 하는 결정적인 이유가 또 하나 존재한다. 앞서 다중 분류 문제는 기본적으로 이중 분류 문제 여러 개를 동시에 푸는 방법으로 접근한다고 이야기했었다. 소프트맥스 함수의 출력은 각각의 요소가 0에서 1 사이의 실수이고 총합이 1인 벡터이다. 또한 각 요소의 값이 해당하는 클래스로의 분류에 가지는 신뢰도라고 했으니, 각각에 대해 교차 엔트로피 손실 을 계산할 수 있을 것이다.
각각의 클래스에 대해 교차 엔트로피 손실을 계산하려면 정답 데이터의 형태가 바뀌어야 한다. 교차 엔트로피 손실을 계산하려면 정답 데이터가 0 또는 1이어야 하므로, 아래와 같이 정답을 벡터로 변환 해서 각 클래스로의 분류에 대한 교차 엔트로피를 계산해낼 수 있다.

그림에서 보이는 정답 벡터는 1번 클래스가 정답 임을 나타낸다. 분류할 클래스 개수만큼의 길이를 가지는 정답 벡터로 변환한 것이다. 정답 클래스만 값이 1이고 나머지는 모두 0인 벡터이다. 이런 벡터를 원 핫 벡터(One-hot vector) 라고 한다. 정답 클래스에 대한 요소 하나만 1로 켜져 있다고 해서 이러한 이름이 붙었다.
이제 자연스럽게 소프트맥스 함수를 이용한 다중 분류 모델의 손실 함수를 정의할 수 있다. 소프트맥스 함수를 거친 모델의 출력 벡터와 원 핫 벡터 형태의 정답 데이터 사이에서 계산된 모든 교차 엔트로피 손실의 합 으로 정의된다. 클래스 개수가 \(n\)개인 다중 분류 모델의 손실 함수는 다음과 같이 정의된다.

교차 엔트로피를 계산하는 수식은 그대로이다. 단지 \(n\)개의 요소에 대한 총합으로 확장했을 뿐이다.
PyTorch에서 다중 분류 모델의 손실 함수는 torch.nn.CrossEntropyLoss 메소드로 구현할 수 있다. 저 메소드 안에 소프트맥스 활성 함수가 포함되어 있으므로, 메소드의 입력으로 소프트맥스 함수를 거치지 않은 모델의 원래 출력 벡터가 들어가야 한다.
모델 정의하기
다룰 데이터의 양도 많아졌으니, 본격적으로 신경망을 쌓아서 학습시켜보자. 가장 간단하게 만든다면 다음과 같이 하나의 선형 함수로만 구현할 수도 있을 것이다. PyTorch에서 소프트맥스 함수는 torch.nn.Softmax 메소드를 사용한다.
import torch.nn as nn
model = nn.Sequencial(
nn.Linear(4, 4),
nn.Softmax()
)
그러나 앞서 말했다시피 우리가 사용할 손실 함수인 torch.nn.CrossEntropyLoss 메소드에 소프트맥스 활성 함수가 포함되어 있으므로, 모델의 구현에는 소프트맥스 활성 함수를 포함시키지 않아도 된다.
model = nn.Linear(4, 4)
단순한 모델인 만큼 높은 정확도를 기대하기 힘들다. 복잡해진 입출력 데이터 사이의 관계를 이해하기 위해서, 여러 선형 함수 레이어를 쌓아서 심층 신경망을 만들어보자.
model = nn.Sequential(
nn.Linear(4, 32),
nn.ReLU(),
nn.Linear(32, 32),
nn.ReLU(),
nn.Linear(32, 4)
)
여러 개의 은닉층을 쌓은 신경망 모델을 정의했다. 길이가 4인 입력 벡터가 model에 입력되면, 선언된 순서대로 은닉층과 활성 함수들을 거친 후 길이가 4인 출력 벡터를 만든다. 각 은닉층 사이의 활성 함수로는 ReLU를 사용했으며, 마지막 레이어의 출력은 이후 소프트맥스 함수를 거치게 된다.
한 가지 주목할 점은 시그모이드가 아닌 ReLU(Rectified Linear Unit) 활성 함수를 사용했다는 점이다. ReLU는 다음과 같이 생긴 활성 함수다. 음수인 입력에 대해서는 무조건 0을 출력하고, 양수인 입력은 그대로 출력한다. 정말 단순한 활성 함수지만 모델 최적화에 있어 강력한 성능을 보여준다. 또한 ReLU의 자리를 시그모이드로 대체하면 모델이 잘 학습되지 않는다. 심층 신경망의 학습 과정에서 기인하는 문제인데, 바로 다음에 살펴보도록 하자.

역전파 알고리즘을 통한 심층 신경망의 학습
실제로 다층 신경망 모델을 학습해야 할 시간이 왔다. 모델의 최적화에는 경사 하강법 을 계속 사용하고 있다. 경사 하강법은 이전 챕터에서 구현해본 이중 분류 모델과 같이 하나의 레이어만을 가지고 있는 모델에 대해서는 잘 동작했다. 손실의 계산에 관여하는 레이어가 하나밖에 없었기 때문이다. 그래서 모델 내의 파라미터가 손실에 미치는 영향을 직접 구해낼 수 있었다. 다시 말해서, 각 파라미터에 대한 그래디언트를 직접 계산할 수 있었다.
그러나 모델의 레이어가 두 개 이상으로 늘어나면, 앞쪽 레이어의 파라미터에 대해서는 경사 하강법을 시행하기 어렵게 된다. 중간 레이어들의 계산 결과가 앞쪽 레이어들의 파라미터에 영향을 받기 때문이다. 때문에 앞쪽 레이어의 파라미터들이 손실 함수에 직접적인 영향을 주지 않는다. 그래서 앞쪽 레이어의 파라미터에 대한 그래디언트를 바로 구할 수 없다. 손실 함수는 항상 모든 레이어를 거친 모델의 출력만을 가지고 계산되기 때문에, 어느 하나의 레이어 파라미터만으로 인한 손실 함수의 변화를 바로 파악할 수 없는 것이다. 앞쪽 레이어의 파라미터에도 경사 하강법을 적용하려면, 해당 레이어 이후로 거치는 모든 레이어들에 의한 손실 변화도 동시에 고려해주어야 한다. 따라서 여러 레이어를 쌓은 신경망 모델을 학습하려면 새로운 방법이 필요하다.
이 문제를 해결하지 못하면 다층 신경망 모델을 학습시킬 수 없게 되는 것이고, 딥 러닝은 불가능한 이야기가 된다. 다행히 근 10년간의 방황 끝에 학자들은 다층 신경망의 모든 레이어에 대해 그래디언트를 계산할 수 있는 방법을 찾아냈다. 역전파 라는 이름을 가진 이 알고리즘이 어떻게 모든 레이어에 대한 그래디언트를 계산해서 다층 신경망 모델을 학습시키는지 알아보도록 하자.
역전파 알고리즘의 동작 원리를 이해하기 위해서는 약간의 수학적 기호를 동원함이 불가피하다. 수식을 이해하려기보다, 수학적인 개념을 활용해 어떻게 모델의 파라미터를 업데이트하는지 그 과정에 중점을 두도록 하자.
간단하게 하나의 레이어만을 가지는 모델의 파라미터를 갱신하는 상황을 가정해보자. 계속 강조했듯이, 하나의 레이어는 곧 입출력 관계를 가지는 하나의 함수이다. 편향 파라미터는 제외했을 때, 두 개의 입력 값을 가지는 레이어를 다음처럼 하나의 수학 함수 \(f\)로 표현할 수 있다.
\[\large y = f(x_1, \ x_2) = w_1x_1 + w_2x_2\]수식을 그림으로 표현해보면 아래와 같다.
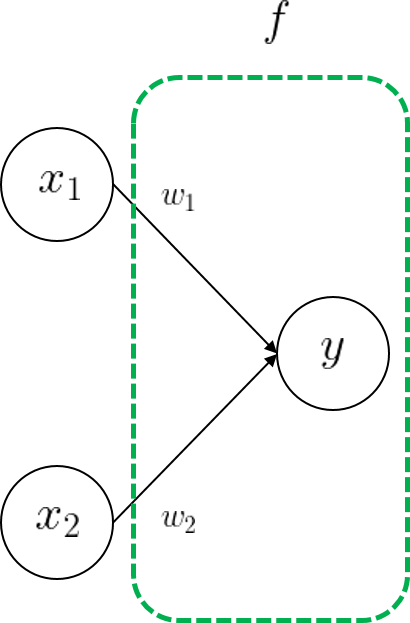
정의한 모델의 출력 \(y\)에 따른 손실 함수를 \(L(y)\)로 정의한다. 모델의 가중치를 한 번 갱신할 때, 현재 손실 값에 따른 파라미터 \(w_1, w_2\)의 그래디언트를 바로 구해낼 수 있다. 구한 그래디언트를 가지고 학습률을 적용해서 파라미터를 갱신한다.
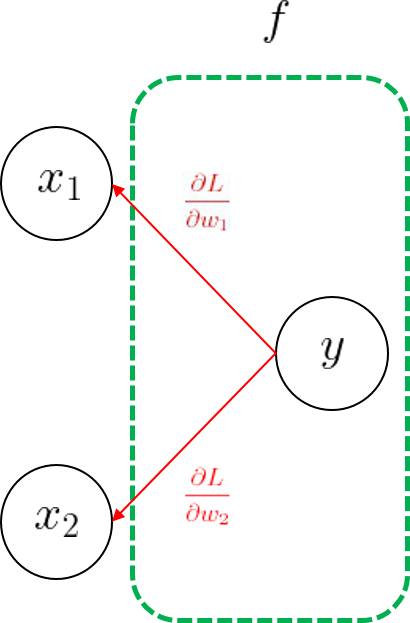
두 개의 파라미터 \(w_1, w_2\)가 직접적으로 손실에 영향을 주기 때문에, 바로 그래디언트를 구할 수 있었다.
이제 복잡한 신경망으로 상황을 확장해보자. 다음의 신경망은 두 개의 은닉층을 가지고 있는 모델이다. 함수 \(f\)의 출력이 그대로 함수 \(g\)에 입력되면 모델의 최종 출력을 만들어낸다.
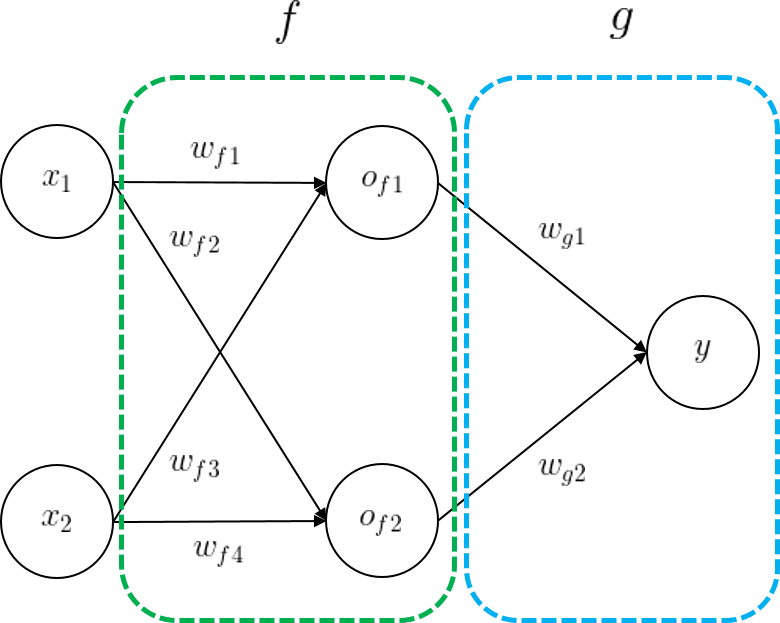
모델의 출력 \(y\)는 함수 \(f\)와 함수 \(g\)를 순서대로 거쳐 만들어진다. 다음과 같이 합성함수 꼴의 수식으로 나타낼 수 있다.
\[\large y = (g \circ f)(x_1, x_2)\]이제 계산된 모델의 손실 \(L(y)\)을 바탕으로 함수 \(g\)와 \(f\)의 모든 파라미터를 업데이트해야 한다. 그를 위해서 모델 내 모든 파라미터 각각에 대한 손실의 미분값을 먼저 구해야 한다. 각각에 경사하강법을 모두 적용해야 하기 때문이다. 모델의 최종 출력을 만드는 레이어인 \(g\)의 파라미터들에 대해서는 미분값을 바로 구할 수 있다. \(g\)의 출력으로 손실을 계산하므로, \(g\)의 파라미터들이 손실에 직접 영향을 주기 때문이다.

문제는 레이어 \(f\) 파라미터의 미분값을 구하려고 할 때 발생한다. 레이어 \(f\)의 출력은 레이어 \(g\)의 경우처럼 손실에 직접적인 영향을 주지 않기 때문이다. 레이어 \(f\) 의 출력이 이후의 레이어들을 거치고 난 후에야 모델의 출력이 만들어지기 때문에, 레이어 \(f\) 파라미터의 미분값은 바로 계산할 수 없다.
레이어 \(f\) 파라미터의 미분값을 계산하기 위해서 연쇄 법칙(Chain rule) 이라는 수학적인 방법을 동원하고자 한다. 연쇄 법칙은 두 개 이상의 함수가 합쳐진 합성 함수를 미분할 때 쓰이는 방법이다. 연쇄 법칙을 사용하면 합성된 각 함수에 대한 미분값을 각각 구해낼 수 있다. 앞서 보았듯이 레이어 두 개를 순서대로 거치는 앞의 모델도 \(y = (g \circ f)(x_1, x_2)\) 모양의 합성 함수로 나타내지므로 연쇄 법칙을 적용할 수 있을 것이다.
연쇄 법칙의 내용은 간단하다. 함수를 거치는 순서의 역으로 함수 사이의 미분을 구하면 된다. 함수 \(y = (g \circ f)(x)\)에서 출력 \(y\)에 대한 입력 \(x\)의 미분을 다음과 같이 구할 수 있다.
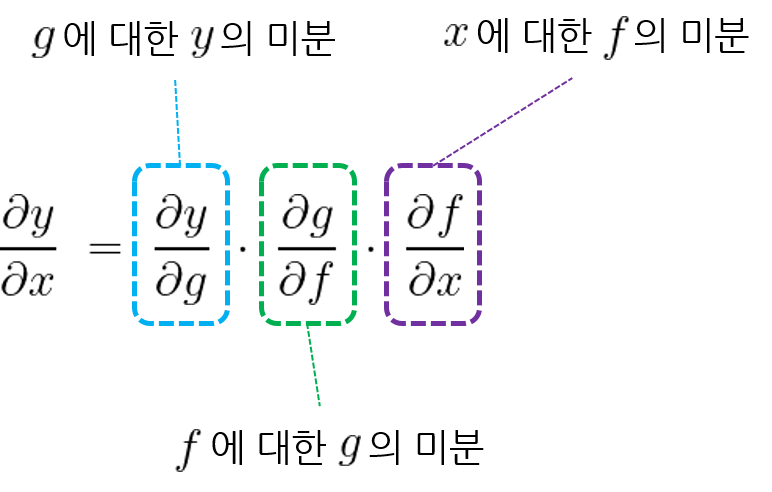
직관적으로 생각하면 쉽다. \(x\)의 입력부터 \(y\)의 출력까지 함수를 거치는 순서는 \(x \ \rightarrow \ f \ \rightarrow \ g \ \rightarrow \ y\)이다. 그러니 미분을 구할 때는 출력 \(y\)부터 역으로 올라가면서 값을 만들어낸 주체가 되는 함수를 미분해나가는 것이다. 각 함수들 사이의 국소적인 미분들을 모두 곱해 합성 함수 전체의 미분을 구하는 것이 연쇄 법칙이다.
다시 예제 모델로 돌아와 보면, 이제 우리는 연쇄 법칙을 이용해 손실 함수 \(L\)에 대한 모든 모델 파라미터들의 미분값을 구할 수 있게 되었다. 하나의 간단한 예로 \(w_{f1}\)에 대한 손실의 미분값을 구해보자.
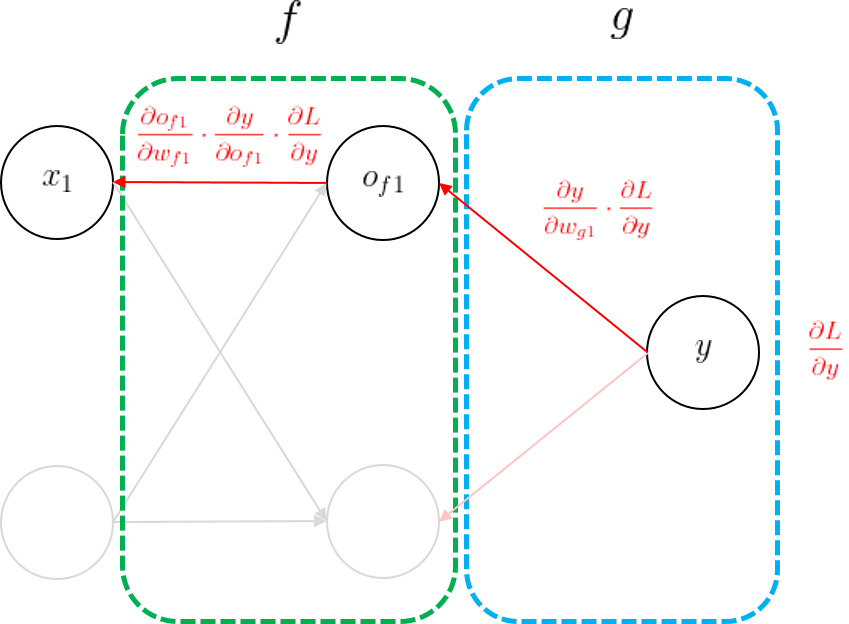
엄밀히 말하면 손실 함수의 입력은 모델의 최종 출력 \(y\)이니, \(y\)에 대한 미분부터 시작하였다. 모델의 출력부터 역순으로 각 레이어의 파라미터들에 대한 레이어 출력의 미분을 구해가면서 $$w_{f1}에 대한 미분까지 도달할 수 있었다. 나머지 모든 파라미터들에 대해서도 같은 방법으로 손실 함수의 미분값을 구할 수 있으며, 경사 하강법을 시행하면 모든 파라미터들을 갱신할 수 있다.
지금까지 살펴본 과정이 다층 신경망 모델 최적화의 핵심 원리이다. 모델에 데이터가 입력될 때부터 출력이 만들어질때까지의 한 과정을 순전파(Forward propagation) 라고 한다. 모든 입력과 은닉층 파라미터들에 대한 순전파 과정을 거쳐 모델의 출력을 만들고 손실을 계산하게 된다. 손실이 계산되면 방금 했던 것처럼 연쇄 법칙에 의해 역순으로 하나씩 모든 파라미터들에 대한 미분값을 만들어낸다. 이 과정을 역전파(Backpropagation) 라고 한다. 순전파를 통해 모델의 손실을 계산하고, 다시 역전파를 통해 모든 파라미터의 그래디언트를 만들어낸다. 역전파 과정이 있어야만 모든 파라미터에 대해 경사하강법을 시행할 수 있다.
우리가 학습할 다중 분류 모델도 동일하게 역전파 알고리즘으로 학습시킬 수 있을 것이다. 우리 모델을 앞에서 했던 것처럼 수식으로 나타내보면 결국 각 레이어들을 순서대로 통과하는 합성 함수의 모습이 보인다.
nn.Linear(4, 32), # f(x)
nn.ReLU(), # relu(x)
nn.Linear(32, 32), # g(x)
nn.ReLU(), # relu(x)
nn.Linear(32, 4) # h(x)
모델의 출력 \(\mathbf{y}\)를 이렇게 표현할 수 있다. \(\mathbf{y}\)로부터 손실을 계산해내기만 하면 역전파 알고리즘을 통해 모든 파라미터의 그래디언트를 구할 수 있다. 실제로는 이후에 소프트맥스 함수가 따로 붙어있으므로, 소프트맥스 함수부터 미분해나가기 시작한다.
역전파 알고리즘이 개발되기 전까지 다층 신경망의 학습은 불가능하다고 여겨졌다. 1980년대 후반까지 신경망 연구가 정체되었던 이유이기도 하다. 역전파 알고리즘은 모델의 레이어나 파라미터의 양에 관계없이 모든 그래디언트를 계산할 수 있다. 하지만 역전파 알고리즘이 다층 신경망 모델 최적화에 항상 만능은 아니다. 특히 쌓인 레이어가 많아질수록 앞쪽 레이어 파라미터가 모델 출력에 미치는 영향이 약해져 학습이 힘들어지는 문제가 크다. 이를 기울기 소실(Vanising Gradient) 문제라고 부른다.
기울기 소실 문제와 ReLU 활성 함수
먼저 결론부터 이야기하자면, 기울기 소실 문제를 해결하기 위해서 다층 신경망 모델 학습에 ReLU 활성 함수를 사용하는 것이 좋다. 기울기 소실 문제의 발생 원인을 먼저 알아보자.
경사 하강법은 현재 파라미터 위치에서의 그래디언트에 따라 파라미터를 갱신하는 과정이고, 이는 모델 파라미터의 변화가 모델 출력과 손실의 변화에 어떤 영향을 미치는지 이해하도록 한다. 그래디언트가 크면 파라미터의 작은 변화에도 모델의 출력이 크게 바뀔 것으로 예상할 수 있다. 문제는 다층 신경망의 사이사이에 적용하는 활성 함수에 있다. 지금까지는 시그모이드 활성 함수를 자주 사용해왔다. 알다시피 시그모이드는 입력 값의 범위에 상관 없이 0에서 1 사이의 작은 범위로 우겨넣은(Squash) 값을 출력한다. 각 레이어 출력의 절댓값이 작을 뿐만 아니라, 모델의 출력 자체도 매우 작은 값을 가진다. 이는 곧 파라미터의 갱신으로 기대되는 모델의 출력 변화량이 작다는 것이고, 그래디언트가 작아질 것임을 예상할 수 있다. 특정 위치에서 그래디언트가 클수록 파라미터의 갱신 폭이 커지는데, 그래디언트가 작으면 항상 갱신 폭이 작아 최적화가 어렵게 된다.
다음의 그림은 시그모이드 함수(파란 실선)와 그 도함수(빨간 점선)의 그래프이다.

역전파 과정을 생각해보자. 모든 레이어 파라미터의 그래디언트를 계산하려면 중간중간의 활성 함수 또한 미분 해주어야 한다. 활성 함수의 출력이 모델의 최종 출력에 미치는 영향도 같이 고려해야 하기 때문이다. 시그모이드 활성 함수의 경우 출력 값이 0 또는 1으로 수렴하기 때문에, 미분했을 때의 그래디언트가 갈수록 작아진다. 역전파는 모델의 뒷쪽 레이어부터 맨 앞 레이어 파라미터의 그래디언트까지 계속 곱해가는 과정인데, 중간중간에 시그모이드 함수를 미분하며 0에 가까운 그래디언트가 계속 곱해지면 결국 앞쪽 레이어로 올 수록 그래디언트가 작아질수밖에 없다. 앞쪽 레이어의 파라미터일수록 모델 출력에 미치는 영향이 작아진다는 것을 증명하는 것이다. 이 현상은 시그모이드로 인해 더욱 두드러지게 나타난다. 이 현상을 두고 그래디언트를 잃어버린다고 하여 기울기 소실 이라고 부른다.
문제 상황을 반대로 생각해보면, 기울기 소실 문제를 해결하는 가장 확실한 방법은 각 레이어의 파라미터 변화가 모델의 최종 출력에 최대한 큰 영향을 미치도록 만드는 것이다. 기울기 소실 문제가 발생하는 가장 큰 이유가 시그모이드 활성 함수의 사용이라고 했으므로, 출력 값을 작은 범위로 우겨넣지 않는 활성 함수로 변경하는 것이 제일 합리적인 해결 방안으로 보인다.
그래서 ReLU 함수가 등장했다. ReLU 함수는 출력 값의 상한이 없다. 파라미터의 작은 변경으로 인한 레이어 출력의 차이가 줄어들지 않고 순전파 과정에 그대로 전달되는 것이다. 또한 미분의 결과도 매우 단순해서, ReLU의 출력이 음수면 그래디언트가 0이고 양수면 1이다. 역전파 과정에서 뒷쪽 레이어 파라미터의 그래디언트에 그대로 1을 곱해 전달하므로, 앞쪽 레이어까지 비교적 큰 그래디언트가 전달될 수 있다.
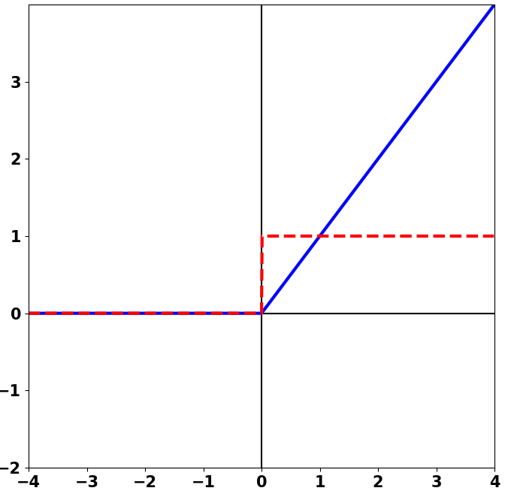
ReLU 함수는 경사하강법을 기반으로 한 다층 신경망 학습의 가능성을 열었다. 꽤나 오래 전에 제안된 활성 함수임에도 불구하고 아직도 수많은 모델에 활용되고 있다. 물론 ReLU도 만능 함수는 아니다. 얼마 가지 않아 ReLU 함수의 문제가 발견되었고, 그것을 해결하기 위한 다양한 방법이 추가로 제시되었다. 그러나 아직까지 대부분의 딥 러닝 모델에서 ReLU 활성 함수는 유용하다. 왜 ReLU가 강력한지 확실하게 이해했기를 바란다.
3.4.2. 모델 학습하기
다층 신경망 모델 학습을 위한 이론적인 배경을 알아보았으니, PyTorch로 직접 우리의 다중 분류 모델을 구현하여 학습해보자.
데이터 준비하고 정규화하기
데이터셋을 읽어오고 매 반복마다 모델에게 배치를 제공하는 작업은 3.3챕터에서 구현했던 FoodDataset의 구조를 그대로 사용해 구현한다. 다만 음식 이름에 따라 4개의 클래스를 0, 1, 2, 3으로 나타내어 주는 부분만 변경하였다.
또한 Min-Max Scaler를 구현하여 입력 데이터를 정규화한다. 실질적으로 관찰될 수 있는 각 데이터의 최솟값이 0인 점을 이용해서, 특징 값들을 해당 특징의 최댓값으로 나누어 구현하도록 하자. 정규화를 위한 normalize_datas 함수를 코드로 구현하면 다음과 같이 구현된다.
def normalize_datas(self):
for i in range(self.x_datas.shape[1]):
col_max = max(self.x_datas[:, i])
self.x_datas[:, i] = (self.x_datas[:, i] / col_max)
이제 normalize_datas 함수를 적용하여 FoodDataset을 구현하자.
import csv
import numpy as np
import torch
from torch.utils.data import Dataset, DataLoader
# 음식 이름에 따라 정답 클래스의 번호를 부여한다.
CLASSES = {
'beverages': 0,
'meats': 1,
'snacks': 2,
'desserts': 3
}
class FoodDataset(Dataset):
def __init__(self, csv_filename):
# CSV 파일 내의 전체 데이터셋 로딩
self.x_datas, self.y_datas = self.data_reader(csv_filename)
self.data_count = len(self.x_datas)
# 데이터셋의 총 길이를 반환하는 메소드
def __len__(self):
return self.data_count
# 모델 입력 데이터와 정답 데이터 쌍을 반환하는 메소드
def __getitem__(self, idx):
# PyTorch 텐서로 바꾸어 반환
tensor_x = torch.as_tensor(self.x_datas[idx])
tensor_y = torch.as_tensor(self.y_datas[idx]).long()
return tensor_x, tensor_y
# CSV 파일에서 데이터를 읽어오는 메소드
def data_reader(self, csv_filename):
csvfile = open(csv_filename, 'r')
reader = csv.reader(csvfile)
x_list, y_list = [], []
for row in reader:
class_name = row[0] # 각 행의 0번째 열은 클래스 이름
xdata = [float(num) for num in row[1:]] # 모델 입력 데이터
ydata = CLASSES[class_name] # 음식 이름에 따른 정답 데이터
x_list.append(xdata) # 입력 데이터 리스트에 추가
y_list.append(ydata) # 정답 데이터 리스트에 추가
# numpy 배열로 바꾸어 반환
x_list = np.array(x_list, dtype=np.float32)
y_list = np.array(y_list, dtype=np.int)
return x_list, y_list
실제로 모델이 학습할 때에 0, 1, 2, 3의 정답 데이터가 원 핫 벡터로 변환되어 사용될 것이다.
모델과 최적화 기법 정의하기
세 개의 레이어를 가지는 다층 신경망 모델을 학습시킬 것이다. 다중 분류를 위한 교차 엔트로피 손실 함수가 사용되고, 최적화 기법으로는 배치 경사하강법(SGD)이 사용된다. 학습률은 0.001이 적당하다.
model = nn.Sequential(
nn.Linear(4, 32),
nn.ReLU(),
nn.Linear(32, 32),
nn.ReLU(),
nn.Linear(32, 4)
)
def train(model):
lf = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
모델 학습하기
학습에 필요한 하이퍼 파라미터들을 정의해주자. 배치 크기는 256, 반복할 에폭의 수는 1,000으로 한다.
batch_size = 256
max_epochs = 1000
미리 정의한 FoodDataset을 사용하는 DataLoader를 선언하고, 최적화 반복을 실행해보자.
dataset = FoodDataset('./assets/datasets/openfoodfacts/openfoodfacts_multi_train_w_dessert.csv')
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
loss_sum = 0
for epoch in range(max_epochs):
x_data = None
for batch_num, samples in enumerate(dataloader):
# 학습 데이터의 한 배치를 불러와 모델의 출력을 얻고 손실을 계산한다.
x_data, y_data = samples
predict = model(x_data)
loss = lf(predict, y_data)
loss_sum += loss.item()
# 계산된 손실로 최적화를 한 스텝 진행한다.
# 이 과정에서 역전파 알고리즘을 통해 모든 파라미터의 그래디언트가 계산된다.
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 매 에폭마다 평균 손실 확인
avg_loss = loss_sum / batch_num
print('Epoch : {}, Current loss : {}'.format(epoch, avg_loss))
loss_sum = 0.0
손실이 정상적으로 감소하면서 학습이 진행되는 모습을 볼 수 있다.
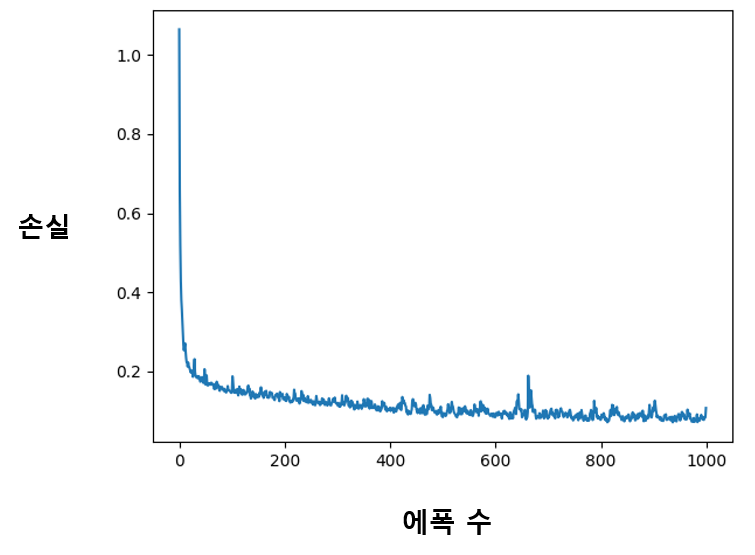
학습한 모델로 추론 실행하기
학습한 다중 분류 모델을 이용해 실제로 분류 결과를 얻어내는 함수를 구현하자.
def inference(model, data):
preds = model(data) # 모델의 출력을 얻는다.
preds = F.softmax(preds, dim=1) # Softmax를 적용한다.
argmax_preds = preds.argmax(dim=1) # 출력 벡터에서 가장 값이 큰 위치를 찾는다.
return argmax_preds
모델에는 소프트맥스 함수가 포함되어있지 않으므로 모델의 출력에 소프트맥스 함수를 따로 적용해주어야 한다. 그렇게 만들어진 출력 벡터에서 argmax 함수를 이용해 가장 값이 큰 요소의 위치를 찾는다. 0, 1, 2, 3의 클래스로 만든 원 핫 벡터를 이용해 학습했으므로, 출력 벡터에서도 가장 값이 큰 위치를 찾으면 해당 클래스로 분류된 것으로 볼 수 있다. 이렇게 우리 모델이 입력 데이터를 어떤 음식으로 구분했는지 알아낼 수 있게 되었다.
3.4.3. 학습 결과 평가하기
미리 준비한 평가 데이터셋으로 학습 결과를 평가해보자.
분류 정확도로 평가하기
다중 분류 문제에서 이용할 수 있는 여러 가지 평가 지표가 있지만, 클래스의 개수가 많지 않고 문제가 간단하므로 단순 분류 정확도(Accuracy) 만을 이용해 모델을 평가하도록 하겠다. 이중 분류에서의 그것과 동일하게, 정답 데이터와 같은 클래스로 분류에 성공한 비율을 측정하면 된다.
정확도 = 분류 성공 개수 / 전체 데이터 개수
정확도를 계산하는 함수를 구현해보자. 모델 추론 결과와 정답 데이터가 같은지 확인하고 그 비율을 계산한다.
def calc_accuracy(inf_result, y_data):
correct_count = 0
bsize = len(inf_result)
for i in range(bsize):
if inf_result[i] == y_data[i]: # 모델의 추론이 맞았을 경우
correct_count += 1
avg_accuracy = float(correct_count) / float(bsize)
return avg_accuracy
이제 평가 데이터셋 전체에 대한 모델의 정확도를 구해보자. 평가 데이터셋도 FoodDataset을 동일하게 사용하여 불러온다. 평가 데이터셋이 크지 않으니 전체 데이터를 한꺼번에 불러와 정확도를 계산한다.
def test(model):
dataset = FoodDataset('./assets/datasets/openfoodfacts/openfoodfacts_multi_test_w_dessert.csv')
dataloader = DataLoader(dataset, batch_size=len(dataset), shuffle=True)
x_data, y_data = next(iter(dataloader))
preds = inference(model, x_data)
accuracy = calc_accuracy(preds, y_data)
print('Accuracy: {}'.format(accuracy))
모델의 학습 후 test 함수를 순서대로 실행해 보면, 90% 이상의 높은 정확도를 볼 수 있다.
Accuracy: 0.93